Advertisements
Advertisements
प्रश्न
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
उत्तर
Given:
Velocity of the source \[v_s\] = 170 m/s
Frequency of the source \[f_0\] = 1200Hz
(a)
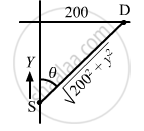
As shown in the figure,
the time taken by the sound to reach the listener is the same as the time taken by the sound to reach the point of intersection.
\[\frac{y}{170} = \frac{\sqrt{{200}^2 + y^2}}{340}\]
\[ \Rightarrow \left( 2y \right)^2 = \left( 200 \right)^2 + \left( y \right)^2 \]
\[ \Rightarrow 4 y^2 - \left( y \right)^2 = \left( 200 \right)^2 \]
\[ \Rightarrow 3 \left( y \right)^2 = \left( 200 \right)^2 \]
\[ \Rightarrow y = \frac{200}{\sqrt{3}}\]
Frequency of source will be :
\[v_s \cos\theta\] = \[170 . \frac{y}{\sqrt{{200}^2 + y^2}} = 170 \times \frac{1}{2} = 85\]
The frequency of sound \[\left( f \right)\] heard by the detector is given by :
\[f = \frac{v}{v - v_s \cos v} \times f_0 \]
\[ \Rightarrow f = \frac{340}{340 - 170 \times \frac{1}{2}} \times 1200\]
\[ \Rightarrow f = 1600 \text{ Hz }\]
(b) The detector will detect a frequency of 1200 Hz at a minimum distance.
\[\frac{200}{340} = \frac{x}{170}\]
\[ \Rightarrow x = 100 \text { m }\]
∴ Distance
\[= \sqrt{\left( 200 \right)^2 + x^2} = \sqrt{\left( 200 \right)^2 + \left( 100 \right)^2}\]
\[ = 224 \text{ m }\]
APPEARS IN
संबंधित प्रश्न
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
A tuning fork sends sound waves in air. If the temperature of the air increases, which of the following parameters will change?
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
At what temperature will the speed of sound be double of its value at 0°C?
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
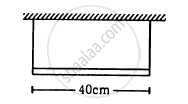
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.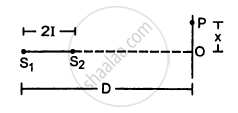
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
With propagation of longitudinal waves through a medium, the quantity transmitted is ______.
Which of the following statements are true for wave motion?
