Advertisements
Advertisements
प्रश्न
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
उत्तर
Given:
Speed of sound in air v = 340 ms−1
Frequency of whistles \[f_0\]= 500 Hz
Speed of train \[v_s\]= 72 km/h =\[72 \times \frac{5}{18} = 20 \text { m/s }\]
The person will receive the sound in a direction that makes an angle θ with the track. The angle θ is given by :
\[\theta = \tan^{- 1} \left( \frac{0 . 5}{2 . 4/2} \right) = 22 . 62^\circ\]
The velocity of the source will be 'v cos θ' when heard by the observer.
So, the apparent frequency received by the man from train A is
\[f_1 = \left( \frac{v}{v - v_s \cos\theta} \right) \times f_0 \]
\[ \Rightarrow f_1 = \left( \frac{340}{340 - v_s \cos 22 . {62}^\circ} \right) \times 500\]
\[ \Rightarrow f_1 = \left( \frac{340}{340 - 20 \times \cos 22 . 62^\circ} \right) \times 500\]
\[ \Rightarrow f_1 = 528 . 70 \text{ Hz } \approx 529 \text { Hz }\]
The apparent frequency heard by the man from train B is
\[f_2 = \left( \frac{v}{v + v\cos\theta} \right) \times f_0 \]
\[ \Rightarrow f_2 = \left( \frac{340}{340 + 20 \times \cos 22 . 62^\circ} \right) \times 500\]
\[ \Rightarrow f_2 = 474 . 24 \text { Hz } \approx 474 \text { Hz }\]
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
When sound wave is refracted from air to water, which of the following will remain unchanged?
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
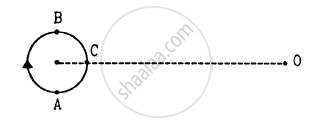
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
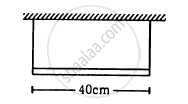
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
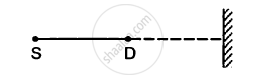
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
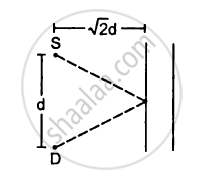
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
Which of the following statements are true for wave motion?
