Advertisements
Advertisements
Question
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
Solution
Given:
Velocity of the source \[v_s\] = 170 m/s
Frequency of the source \[f_0\] = 1200Hz
(a)
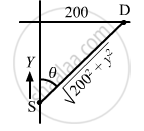
As shown in the figure,
the time taken by the sound to reach the listener is the same as the time taken by the sound to reach the point of intersection.
\[\frac{y}{170} = \frac{\sqrt{{200}^2 + y^2}}{340}\]
\[ \Rightarrow \left( 2y \right)^2 = \left( 200 \right)^2 + \left( y \right)^2 \]
\[ \Rightarrow 4 y^2 - \left( y \right)^2 = \left( 200 \right)^2 \]
\[ \Rightarrow 3 \left( y \right)^2 = \left( 200 \right)^2 \]
\[ \Rightarrow y = \frac{200}{\sqrt{3}}\]
Frequency of source will be :
\[v_s \cos\theta\] = \[170 . \frac{y}{\sqrt{{200}^2 + y^2}} = 170 \times \frac{1}{2} = 85\]
The frequency of sound \[\left( f \right)\] heard by the detector is given by :
\[f = \frac{v}{v - v_s \cos v} \times f_0 \]
\[ \Rightarrow f = \frac{340}{340 - 170 \times \frac{1}{2}} \times 1200\]
\[ \Rightarrow f = 1600 \text{ Hz }\]
(b) The detector will detect a frequency of 1200 Hz at a minimum distance.
\[\frac{200}{340} = \frac{x}{170}\]
\[ \Rightarrow x = 100 \text { m }\]
∴ Distance
\[= \sqrt{\left( 200 \right)^2 + x^2} = \sqrt{\left( 200 \right)^2 + \left( 100 \right)^2}\]
\[ = 224 \text{ m }\]
APPEARS IN
RELATED QUESTIONS
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
A source of sound moves towards an observer.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
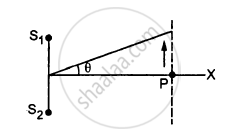
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
