Advertisements
Advertisements
Question
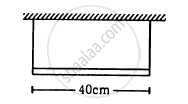
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
Solution
Given:
Length of the rod (L) = 40 cm = 0.40 m
Mass of the rod (m) = 1.2 kg
Let the mass of 4.8 kg be placed at x distance from the left.
As per the question, frequency on the left side = f0
Frequency on the right side = 2f0
Let tension be T1 and T2 on the left and the right side, respectively.
\[\therefore \frac{1}{2L}\sqrt{\frac{T_1}{m}} = \frac{2}{2L}\sqrt{\frac{T_2}{m}}\]
\[ \Rightarrow \sqrt{\frac{T_1}{T_2}} = 2\]
\[ \Rightarrow \frac{T_1}{T_2} = 4 . . . (1)\]
From the free body diagram: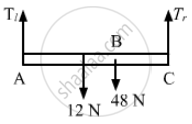
\[T_1 + T_2 = 48 + 12 = 60 N\]
\[ \Rightarrow 4 T_2 + T_2 = 5 T_2 = 60 N \left[ \text{ using equation } \left( 1 \right) \right]\]
\[ \therefore T_2 = 12 N\]
\[\text{ and } T_1 = 48 N\]
Now, taking moment about point A: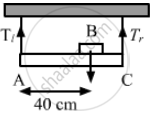
\[T_2 \times \left( 0 . 4 \right) = 48x + 12 \times 0 . 2\]
\[ \Rightarrow 4 . 8 = 48x - 2 . 4\]
\[ \Rightarrow 4 . 8x = 2 . 4\]
\[ \Rightarrow x = \frac{2 . 4}{4 . 8} = \frac{1}{20} m = 5 \text{ cm }\]
Therefore, the mass should be placed at a distance of 5 cm from the left end.
APPEARS IN
RELATED QUESTIONS
What is the smallest positive phase constant which is equivalent to 7⋅5 π?
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
If the sound level in a room is increased from 50 dB to 60 dB, by what factor is the pressure amplitude increased?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
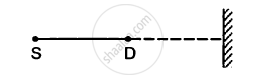
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
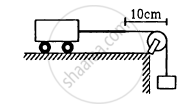
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A source of sound emitting a 1200 Hz note travels along a straight line at a speed of 170 m s−1. A detector is placed at a distance 200 m from the line of motion of the source. (a) Find the frequency of sound receive by the detector at the instant when the source gets closest to it. (b) Find the distance between the source and the detector at the instant in detects the frequency 1200 Hz. Velocity of sound in air = 340 m s−1.
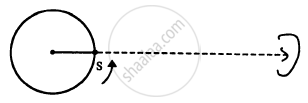
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
With propagation of longitudinal waves through a medium, the quantity transmitted is ______.
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
