Advertisements
Advertisements
Question
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
Solution
Given :
Frequency of source f = 600 Hz
Speed of sound in air v = 330 m/s
\[v = f\lambda\]
\[\therefore \lambda = \frac{v}{f}\]=\[\frac{330}{600} = 0 . 5 \text { mm }\]
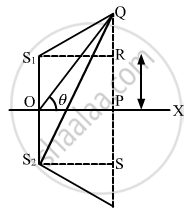
Let the man travel a distance of \[\left( y \right)\]parallel to the y-axis and let \[\left( d \right)\] be the distance between the two speakers. The man is standing at a distance of \[\left( D \right)\]from the origin.
The path difference (x) between the two sound waves reaching the man is given by :
\[x = S_2 Q - S_1 Q = \frac{yd}{D}\]
Angle made by man with the origin :
\[\theta = \frac{y}{D}\]
Given:
d = 2 m
(a) For minimum intensity:
The destructive interference of sound (minimum intensity) takes place if the path difference is an odd integral
multiple of half of the wavelength.
\[\therefore x = (2n + 1)\left( \frac{\lambda}{2} \right)\]
\[\text { For } \left( n = 0 \right)\]
\[ \therefore \frac{yd}{D} = \frac{\lambda}{2}\]
\[\left( \because \theta = \frac{y}{D} \right)\]
\[ \therefore \theta d = \frac{\lambda}{2}\]
\[ \therefore \theta = \frac{\lambda}{2d} = \frac{0 . 55}{4} = 0 . 1375 \text{ rad }\]
\[ \Rightarrow \theta = 0 . 1375 \times (57 . 1)^\circ= 7 . 9^\circ\]
(b) For maximum intensity:
The constructive interference of sound (maximum intensity) takes place if the path difference is an integral multiple of the wavelength.
\[x = n\lambda\]
\[\text { For } \left( n = 1 \right): \]
\[ \Rightarrow \frac{yd}{D} = \lambda\]
\[ \Rightarrow \theta = \frac{\lambda}{d}\]
\[ \Rightarrow \theta = \frac{0 . 55}{2} = 0 . 275 \text { rad }\]
\[ \therefore \theta = 16^\circ\]
(c) The more number of maxima is given by the path difference :
\[\frac{yd}{D} = 2\lambda, 3\lambda, 4\lambda, . . . . . \]
\[ \Rightarrow \frac{y}{D} = \theta = 32^\circ, 64^\circ, 128^\circ\]
He will hear two more maxima at 32° and 64° because the maximum value of θ may be 90°.
APPEARS IN
RELATED QUESTIONS
Explain what is Doppler effect in sound
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When sound wave is refracted from air to water, which of the following will remain unchanged?
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
When two waves with same frequency and constant phase difference interfere,
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A source of sound moves towards an observer.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.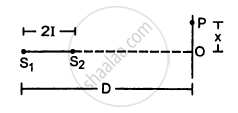
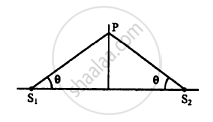
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
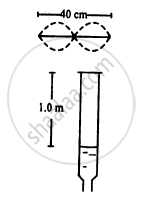
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
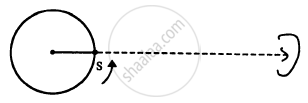
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
Which of the following statements are true for wave motion?
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
