Advertisements
Advertisements
Question
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
Options
`y = 0.6 sin 2π (t + x/2)`
`y = - 0.4 sin 2π (t + x/2)`
`y = 0.4 sin 2π (t + x/2)`
`y = - 0.4 sin 2π (t - x/2)`
Solution
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is `underline(y = - 0.4 sin 2π (t + x/2))`.
Explanation:
The amplitude of a reflected wave `A_r = 2/3 xx A_i = 2/3 xx 0.6` = 0.4 units
Given the equation of incident wave `y_i = 0.6 sin 2π (t - x/2)`
The Equation of reflected wave is `y_i = A_r sin 2π (t + x/2 + π)` ......[∵ At denser medium, phase changes by π]
The positive sign is due to the reversal of direction of the proportion
So, `y_r = - 0.4 sin 2π (t + x/2)` ......[∵ sin(π + θ) = – sinθ]
APPEARS IN
RELATED QUESTIONS
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
When two waves with same frequency and constant phase difference interfere,
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.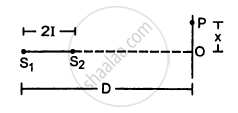
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
Which of the following statements are true for wave motion?
