Advertisements
Advertisements
प्रश्न
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
विकल्प
`y = 0.6 sin 2π (t + x/2)`
`y = - 0.4 sin 2π (t + x/2)`
`y = 0.4 sin 2π (t + x/2)`
`y = - 0.4 sin 2π (t - x/2)`
उत्तर
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is `underline(y = - 0.4 sin 2π (t + x/2))`.
Explanation:
The amplitude of a reflected wave `A_r = 2/3 xx A_i = 2/3 xx 0.6` = 0.4 units
Given the equation of incident wave `y_i = 0.6 sin 2π (t - x/2)`
The Equation of reflected wave is `y_i = A_r sin 2π (t + x/2 + π)` ......[∵ At denser medium, phase changes by π]
The positive sign is due to the reversal of direction of the proportion
So, `y_r = - 0.4 sin 2π (t + x/2)` ......[∵ sin(π + θ) = – sinθ]
APPEARS IN
संबंधित प्रश्न
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
At what temperature will the speed of sound be double of its value at 0°C?
The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
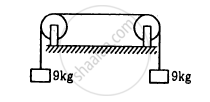
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A sound source, fixed at the origin, is continuously emitting sound at a frequency of 660 Hz. The sound travels in air at a speed of 330 m s−1. A listener is moving along the lien x= 336 m at a constant speed of 26 m s−1. Find the frequency of the sound as observed by the listener when he is (a) at y = − 140 m, (b) at y = 0 and (c) at y = 140 m.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
A small speaker delivers 2W of audio output. At what distance from the speaker will one detect 120 dB intensity sound?
[Given reference intensity of sound as 10-12W/m2]
