Advertisements
Advertisements
प्रश्न
The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
उत्तर
Given:
The absolute temperature of air in a region increases linearly from T1 to T2 in a space of width d.
The speed of sound at 273 K is v.
vT is the velocity of the sound at temperature T.
Let us find the temperature variation at a distance x in the region.
Temperature variation is given by:
\[T = T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \]
\[ v \propto \sqrt{T}\]
\[ \Rightarrow \frac{v_T}{v} = \sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow v_T = v\sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow dt = \frac{dx}{v_T} = \frac{du}{v} \times \sqrt{\left( \frac{273}{T} \right)}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \int\limits_0^d \frac{dx}{\left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \right]^\frac{1}{2}}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1} \left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d} \right]_0^d \]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1}\left( \sqrt{T_2} - \sqrt{T_1} \right)\]
\[ \Rightarrow t = \left( \frac{2d}{v} \right)\left( \frac{\sqrt{273}}{T_2 - T_1} \right) \times \sqrt{T_2} - \sqrt{T_1} \left( \because A^2 - B^2 = \left( A - B \right)\left( A + B \right) \right)\]
\[ \Rightarrow T = \frac{2d}{v}\frac{\sqrt{273}}{\sqrt{T_2} + \sqrt{T_1}} . . . (i)\]
Evaluating this time:
Initial temperature T1 = 280 K
Final temperature T2 = 310 K
Space width d = 33 m
v = 330 m s−1
On substituting the respective values in the above equation, we get:
\[T = \frac{2 \times 33}{330}\frac{\sqrt{273}}{\sqrt{280} + \sqrt{310}} = 96 \text { ms }\]
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
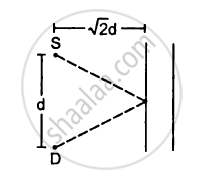
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
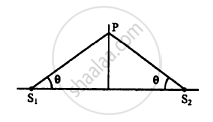
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
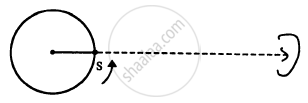
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.