Advertisements
Advertisements
प्रश्न
The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
उत्तर
Given:
The absolute temperature of air in a region increases linearly from T1 to T2 in a space of width d.
The speed of sound at 273 K is v.
vT is the velocity of the sound at temperature T.
Let us find the temperature variation at a distance x in the region.
Temperature variation is given by:
\[T = T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \]
\[ v \propto \sqrt{T}\]
\[ \Rightarrow \frac{v_T}{v} = \sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow v_T = v\sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow dt = \frac{dx}{v_T} = \frac{du}{v} \times \sqrt{\left( \frac{273}{T} \right)}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \int\limits_0^d \frac{dx}{\left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \right]^\frac{1}{2}}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1} \left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d} \right]_0^d \]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1}\left( \sqrt{T_2} - \sqrt{T_1} \right)\]
\[ \Rightarrow t = \left( \frac{2d}{v} \right)\left( \frac{\sqrt{273}}{T_2 - T_1} \right) \times \sqrt{T_2} - \sqrt{T_1} \left( \because A^2 - B^2 = \left( A - B \right)\left( A + B \right) \right)\]
\[ \Rightarrow T = \frac{2d}{v}\frac{\sqrt{273}}{\sqrt{T_2} + \sqrt{T_1}} . . . (i)\]
Evaluating this time:
Initial temperature T1 = 280 K
Final temperature T2 = 310 K
Space width d = 33 m
v = 330 m s−1
On substituting the respective values in the above equation, we get:
\[T = \frac{2 \times 33}{330}\frac{\sqrt{273}}{\sqrt{280} + \sqrt{310}} = 96 \text { ms }\]
APPEARS IN
संबंधित प्रश्न
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
When two waves with same frequency and constant phase difference interfere,
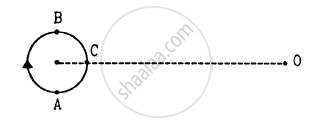
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
The equation of a travelling sound wave is y = 6.0 sin (600 t − 1.8 x) where y is measured in 10−5 m, t in second and x in metre. (a) Find the ratio of the displacement amplitude of the particles to the wavelength of the wave. (b) Find the ratio of the velocity amplitude of the particles to the wave speed.
At what temperature will the speed of sound be double of its value at 0°C?
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?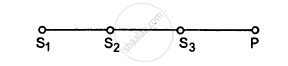
In a standing wave pattern in a vibrating air column, nodes are formed at a distance of 4.0 cm. If the speed of sound in air is 328 m s−1, what is the frequency of the source?
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
