Advertisements
Advertisements
Question
The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
Solution
Given:
The absolute temperature of air in a region increases linearly from T1 to T2 in a space of width d.
The speed of sound at 273 K is v.
vT is the velocity of the sound at temperature T.
Let us find the temperature variation at a distance x in the region.
Temperature variation is given by:
\[T = T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \]
\[ v \propto \sqrt{T}\]
\[ \Rightarrow \frac{v_T}{v} = \sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow v_T = v\sqrt{\left( \frac{T}{273} \right)}\]
\[ \Rightarrow dt = \frac{dx}{v_T} = \frac{du}{v} \times \sqrt{\left( \frac{273}{T} \right)}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \int\limits_0^d \frac{dx}{\left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d}x \right]^\frac{1}{2}}\]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1} \left[ T_1 + \frac{\left( T_2 - T_1 \right)}{d} \right]_0^d \]
\[ \Rightarrow t = \frac{\sqrt{273}}{v} \times \frac{2d}{T_2 - T_1}\left( \sqrt{T_2} - \sqrt{T_1} \right)\]
\[ \Rightarrow t = \left( \frac{2d}{v} \right)\left( \frac{\sqrt{273}}{T_2 - T_1} \right) \times \sqrt{T_2} - \sqrt{T_1} \left( \because A^2 - B^2 = \left( A - B \right)\left( A + B \right) \right)\]
\[ \Rightarrow T = \frac{2d}{v}\frac{\sqrt{273}}{\sqrt{T_2} + \sqrt{T_1}} . . . (i)\]
Evaluating this time:
Initial temperature T1 = 280 K
Final temperature T2 = 310 K
Space width d = 33 m
v = 330 m s−1
On substituting the respective values in the above equation, we get:
\[T = \frac{2 \times 33}{330}\frac{\sqrt{273}}{\sqrt{280} + \sqrt{310}} = 96 \text { ms }\]
APPEARS IN
RELATED QUESTIONS
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
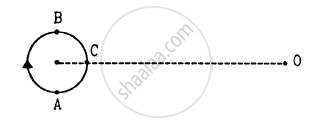
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
The sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source?
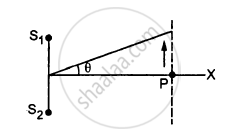
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
Two coherent narrow slits emitting sound of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The sound is detected by moving a detector on the screen ∑ at a distance D(>>λ) from the slit S1 as shown in figure. Find the distance x such that the intensity at P is equal to the intensity at O.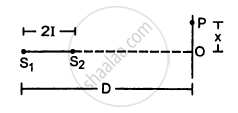
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
A small source of sound oscillates in simple harmonic motion with an amplitude of 17 cm. A detector is placed along the line of motion of the source. The source emits a sound of frequency 800 Hz which travels at a speed of 340 m s−1. If the width of the frequency band detected by the detector is 8 Hz, find the time period of the source.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
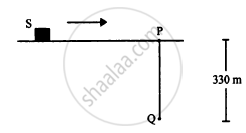
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
Which of the following statements are true for wave motion?
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
In an experiment to determine the velocity of sound in air at room temperature using a resonance tube, the first resonance is observed when the air column has a length of 20.0 cm for a tuning fork of frequency 400 Hz is used. The velocity of the sound at room temperature is 336 ms-1. The third resonance is observed when the air column has a length of ______ cm.
