Advertisements
Advertisements
Question
At what temperature will the speed of sound be double of its value at 0°C?
Solution
Let the speed of sound T1 be v1,
where T1 = 0˚ C = 273 K.
Let T2 be the temperature at which the speed of sound (v2) will be double its value at 0˚ C.
As per the question,
v2 = 2v1.
\[v \propto \sqrt{T}\]
∴
\[\frac{{v_2}^2}{{v_1}^2} = \frac{T_2}{T_1}\]
\[ \Rightarrow \frac{\left( 2 v_1 \right)^2}{{v_1}^2} = \frac{T_2}{273}\]
\[ \Rightarrow T_2 = 273 \times 4 = 1092 K\]
To convert Kelvin into degree celsius:
\[T_2 = \left( 273 \times 4 \right) - 273 = 819^\circ C\]
Hence, the temperature (T2 ) will be 819˚ C
APPEARS IN
RELATED QUESTIONS
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
When two waves with same frequency and constant phase difference interfere,
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
If the intensity of sound is doubled, by how many decibels does the sound level increase?
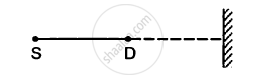
A source of sound S and detector D are placed at some distance from one another. a big cardboard is placed near hte detector and perpendicular to the line SD as shown in figure. It is gradually moved away and it is found that the intensity changes from a maximum to a minimum as the board is moved through a distance of 20 cm. Find the frequency of the sound emitted. Velocity of sound in air is 336 m s−1.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?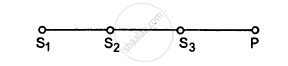
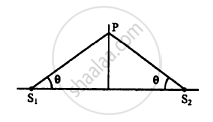
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
Which of the following statements are true for wave motion?
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
A small speaker delivers 2W of audio output. At what distance from the speaker will one detect 120 dB intensity sound?
[Given reference intensity of sound as 10-12W/m2]
