Advertisements
Advertisements
प्रश्न
Sound waves from a loudspeaker spread nearly uniformly in all directions if the wavelength of the sound is much larger than the diameter of the loudspeaker. (a)Calculate the frequency for which the wavelength of sound in air is ten times the diameter of the speaker if the diameter is 20 cm. (b) Sound is essentially transmitted in the forward direction if the wavelength is much shorter than the diameter of the speaker. Calculate the frequency at which the wavelength of the sound is one tenth of the diameter of the speaker described above. Take the speed of sound to be 340 m/s.
उत्तर
Given:
The diameter of the loudspeaker is 20 cm.
Velocity of sound in air v = 340 m/s
As per the question,
wavelength (λ) of the sound is 10 times the diameter of the loudspeaker.
∴ (λ) = 20 cm \[\times 10\]= 200 cm = 2 m
(a) Frequency f = ?
As we know, \[v = f\lambda\]
\[\therefore f = \frac{v}{\lambda} = \frac{340}{2} = 170 Hz\]
(b) Here, wavelength is one tenth of the diameter of the loudspeaker.
⇒ λ = 2 cm = 2 × 10−2 m
\[\therefore f = \frac{v}{\lambda} = \frac{340}{2 \times {10}^{- 2}} = 17, 000 \text{ Hz } = 17 \text{ kHz }\]
APPEARS IN
संबंधित प्रश्न
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
Two loudspeakers are arranged facing each other at some distance. Will a person standing behind one of the loudspeakers clearly hear the sound of the other loudspeaker or the clarity will be seriously damaged because of the 'collision' of the two sounds in between?
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
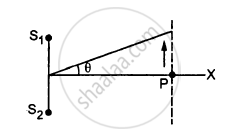
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
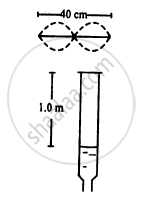
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
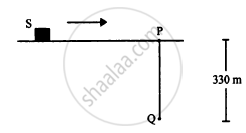
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
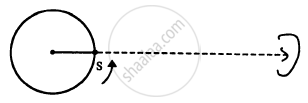
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
