Advertisements
Advertisements
प्रश्न
A tuning fork of frequency 512 Hz is vibrated with a sonometer wire and 6 beats per second are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
पर्याय
506 Hz
512 Hz
518 Hz
524 Hz.
उत्तर
506 Hz

The frequency of the sonometer may be 512 ± 6Hz, i.e., 506 Hz or 518 Hz.
On increasing the tension in a sonometer wire, the velocity of the wave (v) increases proportionately as the number of beats decreases. Therefore, the frequency of the sonometer wire is 506 Hz.
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
Two tuning forks vibrate with the same amplitude but the frequency of the first is double the frequency of the second. Which fork produces more intense sound in air?
When two waves with same frequency and constant phase difference interfere,
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
The fundamental frequency of a vibrating organ pipe is 200 Hz.
(a) The first overtone is 400 Hz.
(b) The first overtone may be 400 Hz.
(c) The first overtone may be 600 Hz.
(d) 600 Hz is an overtone.
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
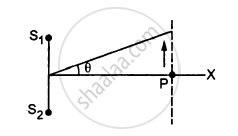
Two speakers S1 and S2, driven by the same amplifier, are placed at y = 1.0 m and y = −1.0 m(See figure). The speakers vibrate in phase at 600 Hz. A man stands at a point on the X-axis at a very large distance from the origin and starts moving parallel to the Y-axis. The speed of sound in air is 330 m s−1. (a) At what angle θ will the intensity of sound drop to a minimum for the first time? (b) At what angle will he hear a maximum of sound intensity for the first time? (c) If he continues to walk along the line, how many more can he hear?
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
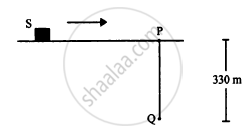
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
