Advertisements
Advertisements
Question
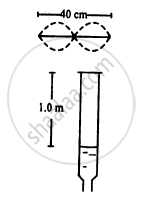
Consider the situation shown in the figure.The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 340 m s−1, find the tension in the wire.
Solution
Given:
Speed of sound in air v = 340 ms−1
Length of the wire l = 40 cm = 0.4 m
Mass of the wire M = 4 g
Mass per unit length of wire \[\left( m \right)\] is given by :
\[m = \frac{\text { Mass }}{\text { Unit length }} = {10}^{- 2} \text { kg/m }\]
\[n_0\]= frequency of the tuning fork
T = tension of the string
Fundamental frequency : \[n_0 = \frac{1}{2L}\sqrt{\frac{T}{m}}\]
For second harmonic,
\[n_1 = 2 n_0\] :
\[n_1 = \frac{2}{2L}\sqrt{\frac{T}{m}} . . . . . \left( i \right)\]
\[n_1 = 2 n_0 = \frac{340}{4} \times 1 = 85 \text { Hz }\]
On substituting the respective values in equation (i), we get :
\[85 = \frac{2}{2 \times 0 . 4}\sqrt{\frac{T}{{10}^{- 2}}}\]
\[ \Rightarrow T = (85 )^2 \times (0 . 4 )^2 \times {10}^{- 2} \]
\[ = 11 . 6 \text { Newton }\]
Hence, the tension in the wire is 11.6 N.
APPEARS IN
RELATED QUESTIONS
Explain what is Doppler effect in sound
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
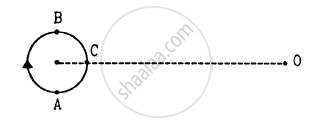
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
A man stands before a large wall at a distance of 50.0 m and claps his hands at regular intervals. Initially, the interval is large. He gradually reduces the interval and fixes it at a value when the echo of a clap merges every 3 seconds, find the velocity of sound in air.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
The absolute temperature of air in a region linearly increases from T1 to T2 in a space of width d. Find the time taken by a sound wave to go through the region in terms of T1, T2, d and the speed v of sound at 273 K. Evaluate this time for T1 = 280 K, T2 = 310 K, d = 33 m and v = 330 m s−1.
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
If the intensity of sound is doubled, by how many decibels does the sound level increase?
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
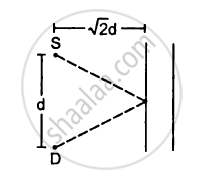
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
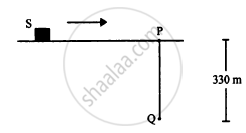
Figure shows a source of sound moving along X-axis at a speed of 22 m s−1continuously emitting a sound of frequency 2.0 kHz which travels in air at a speed of 330 m s−1. A listener Q stands on the Y-axis at a distance of 330 m from the origin. At t = 0, the sources crosses the origin P. (a) When does the sound emitted from the source at P reach the listener Q? (b) What will be the frequency heard by the listener at this instant? (c) Where will the source be at this instant?
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
