Advertisements
Advertisements
Question
A source of sound moves towards an observer.
Options
The frequency of the source is increased.
The velocity of sound in the medium is increased.
The wavelength of sound in the medium towards the observer is decreased.
The amplitude of vibration of the particles is increased.
Solution
The wavelength of the sound in the medium towards the observer decreases.
Due to Doppler effect, the frequency or wavelength of the sound changes towards the observer only.
The actual frequency and wavelength of the source does not change.
APPEARS IN
RELATED QUESTIONS
Explain what is Doppler effect in sound
The wavelengths of two sound waves in air are `81/173`m and `81/170`m. They produce 10 beats per second. Calculate the velocity of sound in air
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
The bulk modulus and the density of water are greater than those of air. With this much of information, we can say that velocity of sound in air
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
Find the minimum and maximum wavelengths of sound in water that is in the audible range (20−20000 Hz) for an average human ear. Speed of sound in water = 1450 m s−1.
A sound wave frequency 100 Hz is travelling in air. The speed of sound in air is 350 m s−1. (a) By how much is the phase changed at a given point in 2.5 ms? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation?
A sources of sound operates at 2.0 kHz, 20 W emitting sound uniformly in all directions. The speed of sound in air is 340 m s−1 and the density of air is 1.2 kg m −3. (a) What is the intensity at a distance of 6.0 m from the source? (b) What will be the pressure amplitude at this point? (c) What will be the displacement amplitude at this point?
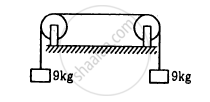
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?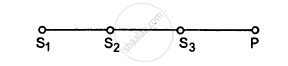
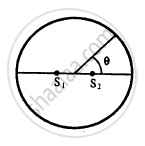
Figure shown two coherent sources S1 and S2 which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S1,S2 is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.
The first overtone frequency of a closed organ pipe P1 is equal to the fundamental frequency of a open organ pipe P2. If the length of the pipe P1 is 30 cm, what will be the length of P2?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
For the propagation of longitudinal waves, the medium must have
- elasticity
- mass
- inertia
- force of cohesion
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
