Advertisements
Advertisements
Question
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
Solution
Given:
Length of the string = L
Velocity of wave is given as:
\[V = \sqrt{\frac{T}{m}}\]
(a) \[\text{Wavelength}, \lambda = \frac{\text{Velocity}}{\text{Frequency}}\]
\[\Rightarrow \lambda = \frac{\sqrt{\frac{T}{m}}}{\frac{1}{2L}\sqrt{\frac{T}{m}}} = 2L\]
\[\text{ Wave number,} K = \frac{2\pi}{\lambda} = \frac{2\pi}{2L} = \frac{\pi}{L}\]
(b) Equation of the stationary wave:
We have `y = Asin (2pix)/lambda * cos(omegat + phi)`
Given, At t = 0
`x = L/2`
y = 0
∴` 0 = Asin (2piL/2)/(2L)cos(0 + phi)`
or cos Φ = 0
or Φ = π/2
Now,
`y = Asin (2pix)/(2L)cos(2 pi f t + pi/2)`
= `Asin(pix)/Lsin(2 pi f t)`
APPEARS IN
RELATED QUESTIONS
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
A string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion? What if the string vibrates in its first overtone?
When sound wave is refracted from air to water, which of the following will remain unchanged?
When two waves with same frequency and constant phase difference interfere,
A source of sound moves towards an observer.
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360 m s−1.
Ultrasonic waves of frequency 4.5 MHz are used to detect tumour in soft tissue. The speed of sound in tissue is 1.5 km s−1 and that in air is 340 m s−1. Find the wavelength of this ultrasonic wave in air and in tissue.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
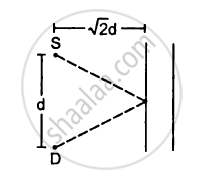
A source S and a detector D are placed at a distance d apart. A big cardboard is placed at a distance \[\sqrt{2}d\] from the source and the detector as shown in figure. The source emits a wave of wavelength = d/2 which is received by the detector after reflection from the cardboard. It is found to be in phase with the direct wave received from the source. By what minimum distance should the cardboard be shifted away so that the reflected wave becomes out of phase with the direct wave?
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?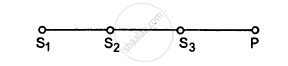
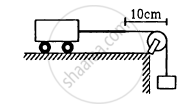
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in following figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the heavy string can resonate?
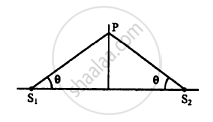
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A source of sound with adjustable frequency produces 2 beats per second with a tuning fork when its frequency is either 476 Hz of 480 Hz. What is the frequency of the tuning fork?
With propagation of longitudinal waves through a medium, the quantity transmitted is ______.
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
The speed of a wave in a string is 20 m/s and the frequency is 50 Hz. The phase difference between two points on the string 10 cm apart will be ______.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
A transverse wave is represented by y = 2sin (ωt - kx) cm. The value of wavelength (in cm) for which the wave velocity becomes equal to the maximum particle velocity, will be ______.
