Advertisements
Advertisements
प्रश्न
A string of length L fixed at both ends vibrates in its fundamental mode at a frequency ν and a maximum amplitude A. (a)
- Find the wavelength and the wave number k.
- Take the origin at one end of the string and the X-axis along the string. Take the Y-axis along the direction of the displacement. Take t = 0 at the instant when the middle point of the string passes through its mean position and is going towards the positive y-direction. Write the equation describing the standing wave.
उत्तर
Given:
Length of the string = L
Velocity of wave is given as:
\[V = \sqrt{\frac{T}{m}}\]
(a) \[\text{Wavelength}, \lambda = \frac{\text{Velocity}}{\text{Frequency}}\]
\[\Rightarrow \lambda = \frac{\sqrt{\frac{T}{m}}}{\frac{1}{2L}\sqrt{\frac{T}{m}}} = 2L\]
\[\text{ Wave number,} K = \frac{2\pi}{\lambda} = \frac{2\pi}{2L} = \frac{\pi}{L}\]
(b) Equation of the stationary wave:
We have `y = Asin (2pix)/lambda * cos(omegat + phi)`
Given, At t = 0
`x = L/2`
y = 0
∴` 0 = Asin (2piL/2)/(2L)cos(0 + phi)`
or cos Φ = 0
or Φ = π/2
Now,
`y = Asin (2pix)/(2L)cos(2 pi f t + pi/2)`
= `Asin(pix)/Lsin(2 pi f t)`
APPEARS IN
संबंधित प्रश्न
Explain what is Doppler effect in sound
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
Can you hear your own words if you are standing in a perfect vacuum? Can you hear your friend in the same conditions?
Two sound waves move in the same direction in the same medium. The pressure amplitudes of the waves are equal but the wavelength of the first wave is double the second. Let the average power transmitted across a cross section by the first wave be P1 and that by the second wave be P2. Then
A source of sound moves towards an observer.
Two point sources of sound are kept at a separation of 10 cm. They vibrate in phase to produce waves of wavelength 5.0 cm. What would be the phase difference between the two waves arriving at a point 20 cm from one source (a) on the line joining the sources and (b) on the perpendicular bisector of the line joining the sources?
Calculate the bulk modulus of air from the following data about a sound wave of wavelength 35 cm travelling in air. The pressure at a point varies between (1.0 × 105 ± 14) Pa and the particles of the air vibrate in simple harmonic motion of amplitude 5.5 × 10−6 m.
A particular guitar wire is 30⋅0 cm long and vibrates at a frequency of 196 Hz when no finger is placed on it. The next higher notes on the scale are 220 Hz, 247 Hz, 262 Hz and 294 Hz. How far from the end of the string must the finger be placed to play these notes?
The two sources of sound, S1 and S2, emitting waves of equal wavelength 20.0 cm, are placed with a separation of 20.0 cm between them. A detector can be moved on a line parallel to S1 S2 and at a distance of 20.0 cm from it. Initially, the detector is equidistant from the two sources. Assuming that the waves emitted by the sources are in detector should be shifted to detect a minimum of sound.
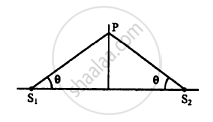
Two sources of sound S1 and S2 vibrate at same frequency and are in phase. The intensity of sound detected at a point P as shown in the figure is I0. (a) If θ equals 45°, what will be the intensity of sound detected at this point if one of the sources is switched off? (b) What will be the answer of the previous part if θ = 60°?
The fundamental frequency of a closed pipe is 293 Hz when the air in it is a temperature of 20°C. What will be its fundamental frequency when the temperature changes to 22°C?
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
In the wave equation
`y = 0.5sin (2pi)/lambda(400t - x)m`
the velocity of the wave will be ______.
