Question

Figure shown two coherent sources S₁ and S₂ which emit sound of wavelength λ in phase. The separation between the sources is 3λ. A circular wire of large radius is placed in such way that S₁,S₂ is at the centre of the wire. Find the angular positions θ on the wire for which constructive interference takes place.

Answer 1

Let the sound waves from the two coherent sources S₁ and S₂ reach the point P.

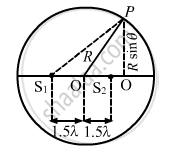
rework
OQ = R cosθ
OP = R cosθ
OS₂ = OS₁ = 1.5\[\lambda\]

From the figure, we find that:

\[P {S_1}^2  = P Q^2  + Q S^2  =  \left( R\sin\theta \right)^2  +  \left( R\cos\theta - 1 . 5\lambda \right)^2\]

\[P {S_1}^2  = P Q^2  + Q {S_1}^2  =  \left( R\sin\theta \right)^2  +  \left( R\cos\theta + 1 . 5\lambda \right)^2\]

Path difference between the sound waves reaching point P is given by:

\[\left( S_1 P \right)^2  -  \left( S_2 P \right)^2  = \left[ \left( R\sin\theta \right)^2 + \left( R\cos\theta  + 1 . 5\lambda \right)^2 \right] - \left[ \left( R\sin\theta \right)^2 + \left( R\cos\theta - 1 . 5\lambda \right)^2 \right]\] 

\[                                             =  \left( 1 . 5\lambda + R\cos\theta \right)^2  -  \left( R\cos\theta - 1 . 5\lambda \right)^2 \] 

\[                                             = 6\lambda R\cos\theta\]

\[\left( S_1 P - S_2 P \right) = \frac{6\lambda R  \cos\theta}{2R}\] 

\[                                     =   3\lambda  \cos\theta\]

Suppose, for constructive interference, this path difference be made equal to the integral multiple of \[\lambda\] .

Hence ,

\[\left( S_1 P - S_2 P \right) = 3\lambda  \cos\theta = n\lambda\] 

\[ \Rightarrow   \cos\theta = \frac{n}{3}\] 

\[ \Rightarrow   \theta =    \cos^{- 1} \left( \frac{n}{3} \right)\]

where, n = 0, 1, 2, ...

⇒ θ = 0°, 48.2°, 70.5°and 90° are similar points in other quadrants.