Advertisements
Advertisements
प्रश्न
A piano wire A vibrates at a fundamental frequency of 600 Hz. A second identical wire Bproduces 6 beats per second with it when the tension in A is slightly increased. Find the the ratio of the tension in A to the tension in B.
उत्तर
Mass per unit length of both the wires = m
Fundamental frequency of wire of length \[\left( l \right)\] and tension \[\left( T \right)\] is given by :
\[n = \frac{1}{2I}\sqrt{\frac{T}{m}}\]
It is clear from the above relation that as the tension increases, the frequency increases.
Fundamental frequency of wire A is given by : \[n_A = \frac{1}{2I}\sqrt{\frac{T_A}{m}}\]
Fundamental frequency of wire B is given by:
\[n_B = \frac{1}{2I}\sqrt{\frac{T_B}{m}}\]
It is given that 6 beats are produced when the tension in A is increased.
⇒ \[n_A = 606 = \frac{1}{2l}\sqrt{\frac{T_A}{m}}\]
Therefore, the ratio can be obtained as:
\[ \frac{n_A}{n_B} = \frac{606}{600} = \frac{\left( 1/2I \right)\sqrt{\left( T_A /m \right)}}{\left( 1/2I \right)\sqrt{T_B /m}}\]
\[ \Rightarrow \frac{606}{600} = \frac{\sqrt{T_A}}{\sqrt{T_B}}\]
\[ \Rightarrow \frac{\sqrt{T_A}}{\sqrt{T_B}} = \frac{606}{600} = 1 . 01\]
\[ \Rightarrow \frac{T_A}{T_B} = 1 . 02\]
APPEARS IN
संबंधित प्रश्न
A wave is represented by an equation \[y = c_1 \sin \left( c_2 x + c_3 t \right)\] In which direction is the wave going? Assume that \[c_1 , c_2\] \[c_3\] are all positive.
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
If you are walking on the moon, can you hear the sound of stones cracking behind you? Can you hear the sound of your own footsteps?
The voice of a person, who has inhaled helium, has a remarkably high pitch. Explain on the basis of resonant vibration of vocal cord filled with air and with helium.
When we clap our hands, the sound produced is best described by Here p denotes the change in pressure from the equilibrium value.
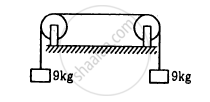
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
The intensity of sound from a point source is 1.0 × 10−8 W m−2 at a distance of 5.0 m from the source. What will be the intensity at a distance of 25 m from the source?
Sound with intensity larger than 120 dB appears pain full to a person. A small speaker delivers 2.0 W of audio output. How close can the person get to the speaker without hurting his ears?
Three sources of sound S1, S2 and S3 of equal intensity are placed in a straight line with S1S2 = S2S3. At a point P, far away from the sources, the wave coming from S2 is 120° ahead in phase of that from S1. Also, the wave coming from S3 is 120° ahead of that from S2. What would be the resultant intensity of sound at P?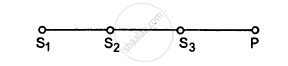
The separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340 m s−1, find the frequency of vibration of the air column.
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
Show that if the room temperature changes by a small amount from T to T + ∆T, the fundamental frequency of an organ pipe changes from v to v + ∆v, where \[\frac{∆ v}{v} = \frac{1}{2}\frac{∆ T}{T} .\]
A cylindrical tube, open at both ends, has a fundamental frequency v. The tube is dipped vertically in water so that half of its length is inside the water. The new fundamental frequency is
Two electric trains run at the same speed of 72 km h−1 along the same track and in the same direction with separation of 2.4 km between them. The two trains simultaneously sound brief whistles. A person is situated at a perpendicular distance of 500 m from the track and is equidistant from the two trains at the instant of the whistling. If both the whistles were at 500 Hz and the speed of sound in air is 340 m s−1, find the frequencies heard by the person.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
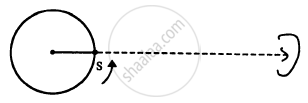
A small source of sound S of frequency 500 Hz is attached to the end of a light string and is whirled in a vertical circle of radius 1.6 m. The string just remains tight when the source is at the highest point. (a) An observer is located in the same vertical plane at a large distance and at the same height as the centre of the circle. The speed of sound in air = 330 m s−1 and g = 10 m s−2. Find the maximum frequency heard by the observer. (b) An observer is situated at a large distance vertically above the centre of the circle. Find the frequency heard by the observer corresponding to the sound emitted by the source when it is at the same height as the centre.
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
During propagation of a plane progressive mechanical wave ______.
- all the particles are vibrating in the same phase.
- amplitude of all the particles is equal.
- particles of the medium executes S.H.M.
- wave velocity depends upon the nature of the medium.
A small speaker delivers 2W of audio output. At what distance from the speaker will one detect 120 dB intensity sound?
[Given reference intensity of sound as 10-12W/m2]
