Advertisements
Advertisements
प्रश्न
The noise level in a classroom in absence of the teacher is 50 dB when 50 students are present. Assuming that on the average each student output same sound energy per second, what will be the noise level if the number of students is increased to 100?
उत्तर
Let the intensity of each student be I and the sound level of 50 students be β1.
if the number of students increases to 100, the sound level becomes β2.
using `beta = 10log_10(I/I_0)`
where I0 is the constant reference intensity, I is the intensity and β is the sound level.
`beta_1 = 10log_10((50I)/I_0)`
`beta_2 = 10log_10((100I)/I_0)`
⇒ `beta_2 - beta_1 = 10log_10((100I)/I_0) - 10log_10((50I)/I_0)`
= `10log_10((100I)/(50I))`
= 10 log10 (2)
= 3
Therefore, the noise level of 100 students
(β2) will be 50 + 3 = 53 dB.
APPEARS IN
संबंधित प्रश्न
The equation \[y = A \sin^2 \left( kx - \omega t \right)\]
represents a wave motion with
A small source of sounds moves on a circle as shown in figure and an observer is sitting at O. Let \[v_1, v_2, v_3\] be the frequencies heard when the source is at A, B and C respectively.
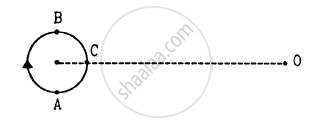
When you speak to your friend, which of the following parameters have a unique value in the sound produced?
An electrically maintained tuning fork vibrates with constant frequency and constant amplitude. If the temperature of the surrounding air increases but pressure remains constant, the produced will have
(a) larger wavelength
(b) larger frequency
(c) larger velocity
(d) larger time period.
A listener is at rest with respect to the source of sound. A wind starts blowing along the line joining the source and the observer. Which of the following quantities do not change?
(a) Frequency
(b) Velocity of sound
(c) Wavelength
(d) Time period
A steel tube of length 1.00 m is struck at one end. A person with his ear closed to the other end hears the sound of the blow twice, one travelling through the body of the tube and the other through the air in the tube. Find the time gap between the two hearings. Use the table in the text for speeds of sound in various substances.
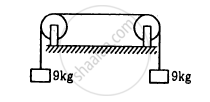
The length of the wire shown in figure between the pulley is 1⋅5 m and its mass is 12⋅0 g. Find the frequency of vibration with which the wire vibrates in two loops leaving the middle point of the wire between the pulleys at rest.
If the intensity of sound is doubled, by how many decibels does the sound level increase?
A string, fixed at both ends, vibrates in a resonant mode with a separation of 2⋅0 cm between the consecutive nodes. For the next higher resonant frequency, this separation is reduced to 1⋅6 cm. Find the length of the string.
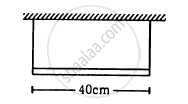
A uniform horizontal rod of length 40 cm and mass 1⋅2 kg is supported by two identical wires as shown in figure. Where should a mass of 4⋅8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone? Take g = 10 m s−2.
A tuning fork produces 4 beats per second with another tuning fork of frequency 256 Hz. The first one is now loaded with a little wax and the beat frequency is found to increase to 6 per second. What was the original frequency of the tuning fork?
A tuning fork of frequency 256 Hz produces 4 beats per second with a wire of length 25 cm vibrating in its fundamental mode. The beat frequency decreases when the length is slightly shortened. What could be the minimum length by which the wire we shortened so that it produces no beats with the tuning fork?
A traffic policeman standing on a road sounds a whistle emitting the main frequency of 2.00 kHz. What could be the apparent frequency heard by a scooter-driver approaching the policeman at a speed of 36.0 km h−1? Speed of sound in air = 340 m s−1.
A boy riding on his bike is going towards east at a speed of 4√2 m s−1. At a certain point he produces a sound pulse of frequency 1650 Hz that travels in air at a speed of 334 m s−1. A second boy stands on the ground 45° south of east from his. Find the frequency of the pulse as received by the second boy.
A train running at 108 km h−1 towards east whistles at a dominant frequency of 500 Hz. Speed of sound in air is 340 m/s. What frequency will a passenger sitting near the open window hear? (b) What frequency will a person standing near the track hear whom the train has just passed? (c) A wind starts blowing towards east at a speed of 36 km h−1. Calculate the frequencies heard by the passenger in the train and by the person standing near the track.
A boy riding on a bicycle going at 12 km h−1 towards a vertical wall whistles at his dog on the ground. If the frequency of the whistle is 1600 Hz and the speed of sound in air is 330 m s−1, find (a) the frequency of the whistle as received by the wall (b) the frequency of the reflected whistle as received by the boy.
A person standing on a road sends a sound signal to the driver of a car going away from him at a speed of 72 km h−1. The signal travelling at 330 m s−1 in air and having a frequency of 1600 Hz gets reflected from the body of the car and returns. Find the frequency of the reflected signal as heard by the person.
A car moves with a speed of 54 km h−1 towards a cliff. The horn of the car emits sound of frequency 400 Hz at a speed of 335 m s−1. (a) Find the wavelength of the sound emitted by the horn in front of the car. (b) Find the wavelength of the wave reflected from the cliff. (c) What frequency does a person sitting in the car hear for the reflected sound wave? (d) How many beats does he hear in 10 seconds between the sound coming directly from the horn and that coming after the reflection?
Equation of a plane progressive wave is given by `y = 0.6 sin 2π (t - x/2)`. On reflection from a denser medium its amplitude becomes 2/3 of the amplitude of the incident wave. The equation of the reflected wave is ______.
