Advertisements
Advertisements
प्रश्न
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
उत्तर
Given:
Speed of sound in air v = 340 ms−1
Distance moved by sliding tube = 2.50 cm
Frequency of sound f = ?
\[\text { Distance between maximum and minimum: } \] \[ \frac{\lambda}{4} = 2 . 50 \text { cm }\]
\[ \Rightarrow \lambda = 2 . 50 \times 4 = 10 \text { cm } = {10}^{- 1} \text { m }\]
As we know,
v = f\[\lambda\].
\[\therefore f = \frac{v}{\lambda}\]
\[ \Rightarrow f = \frac{340}{{10}^{- 1}}=3400\text { Hz }=3.4\text{ kHz }\]
Therefore, the frequency of the sound is 3.4 kHz.
APPEARS IN
संबंधित प्रश्न
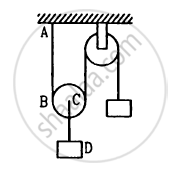
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
The fundamental frequency of a string is proportional to
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
Choose the correct option:
A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
The speed of sound as measured by a student in the laboratory on a winter day is 340 m s−1 when the room temperature is C17°. What speed will be measured by another student repeating the experiment on a day when the room temperature is 32°C?
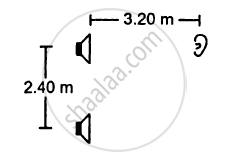
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1. (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train?
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
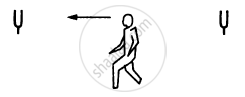
Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
