Advertisements
Advertisements
प्रश्न
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
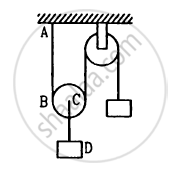
विकल्प
1
2
\[\sqrt{2}\]
\[1/\sqrt{2}\]
उत्तर
\[1/\sqrt{2}\]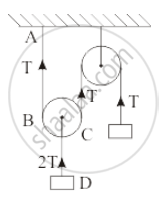
\[T_{AB} = T\]
\[ T_{CD} = 2T\]
where
TAB is the tension in the string AB
TCD is the tension in the string CD
The eelation between tension and the wave speed is given by
\[v = \sqrt{\frac{T}{\mathrm{\mu}}}\]
\[v \propto \sqrt{T}\]
where
v is the wave speed of the transverse wave
μ is the mass per unit length of the string
\[\frac{v_1}{v_2} = \sqrt{\frac{T}{2T}} = \frac{1}{\sqrt{2}}\]
APPEARS IN
संबंधित प्रश्न
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
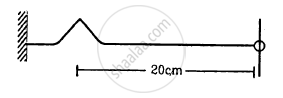
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
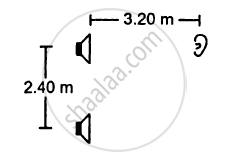
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
A violin player riding on a slow train plays a 440 Hz note. Another violin player standing near the track plays the same note. When the two are closed by and the train approaches the person on the ground, he hears 4.0 beats per second. The speed of sound in air = 340 m s−1. (a) Calculate the speed of the train. (b) What beat frequency is heard by the player in the train?
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
Change in temperature of the medium changes ______.
