Advertisements
Advertisements
प्रश्न
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
उत्तर
Given:
Speed of sound in air v = 332 ms−1
Velocity of the observer \[v_0\]= 3 `\text {ms}^\(-)`1
Velocity of the source \[v_s\]= 0
Frequency of the tuning forks \[f_0\]= 256 Hz
The apparent frequency\[\left( f_1 \right)\] heard by the man when he is running towards the tuning forks is \[f_1 = \left( \frac{v + v_0}{v} \right) \times f_0\]
On substituting the values in the above equation, we get:
\[f_1 = \left( \frac{332 + 3}{332} \right) \times 256 = 258 . 3 \text { Hz }\]
The apparent frequency \[\left( f_2 \right)\] heard by the man when he is running away from the tuning forks is \[f_2 = \left( \frac{v - v_0}{v} \right) \times f_0\]
On substituting the values in the above equation, we get :
\[f_2 = \left( \frac{332 - 3}{332} \right) \times 256\]
\[ = 253 . 7 \text { Hz }.\]
∴ beats produced by them
=\[f_2 - f_1\]
=258.3 − 253.7 = 4.6 Hz
APPEARS IN
संबंधित प्रश्न
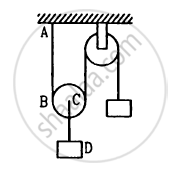
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
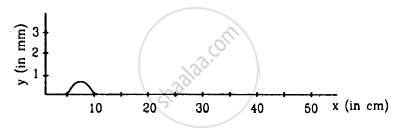
following Figure shows a wave pulse at t = 0. The pulse moves to the right with a speed of 10 cm s−1. Sketch the shape of the string at t = 1 s, 2 s and 3 s.
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
Two tuning forks having frequencies 320 Hz and 340 Hz are sounded together to produce sound waves. The velocity of sound in air is 340 m/s. Find the difference in wavelength of these waves.
