Advertisements
Advertisements
प्रश्न
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
उत्तर
Given:
Speed of bat v = 6 ms−1
Frequency of ultrasonic wave f = 4.5 × 104 Hz
Velocity of bird \[v_s\]= 6 ms−1
Let us assume that the bat is flying between the walls X and Y.
Apparent frequency received by the wall Y is
\[f '_{} = \left( \frac{v}{v - v_s} \right) \times f_0 \]
\[ \Rightarrow f' = \left( \frac{330}{330 - 6} \right) \times 4 . 5 \times {10}^4 \]
\[ \Rightarrow f' = 4 . 58 \times {10}^4 \text { Hz }\]
Now, the apparent frequency received by the bat after reflection from the wall Y is given by :
\[f " = \left( \frac{v + v_s}{v} \right) \times f_x \]
\[ \Rightarrow f " = \left( \frac{330 + 6}{330} \right) \times 4 . 58 \times {10}^4 \]
\[ \Rightarrow f " = 4 . 66 \times {10}^4 \text { Hz }\]
Frequency of ultrasonic wave received by wall X :
\[n' = \frac{330}{330 + 6} \times 4 . 5 \times {10}^4 \]
\[ = 4 . 41 \times {10}^4 \text { Hz }\]
The frequency of the ultrasonic wave received by the bat after reflection from the wall X is
\[n " = \frac{v - v_s}{v} \times n'\]
\[ = \frac{330 - 6}{330} \times 4 . 41 \times {10}^4 \]
\[ = 4 . 33 \times {10}^4 \text{ Hz }\]
Beat frequency heard by the bat is
\[= 4 . 66 \times {10}^4 - 4 . 33 \times {10}^4 \]
\[ = 3300 \text { Hz } .\]
APPEARS IN
संबंधित प्रश्न
Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
Choose the correct option:
A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
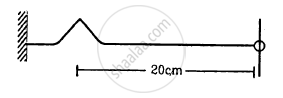
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
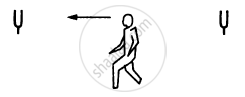
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
An operator sitting in his base camp sends a sound signal of frequency 400 Hz. The signal is reflected back from a car moving towards him. The frequency of the reflected sound is found to be 410 Hz. Find the speed of the car. Speed of sound in air = 324 m s−1
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
