Advertisements
Advertisements
प्रश्न
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
उत्तर
The wave equation is represented by \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right)\]
Let:
Time period = T
Wavelength = λ
\[\left( a \right) T = 2 \times 0 . 01 = 0 . 02 s = 20 ms\]
\[ \lambda = 2 \times 2 = 4 cm\]
(b) Equation for the velocity of the particle:
\[= - 0 . 50 \cos 2\pi\left\{ \left( \frac{x}{4} \right) - \left( \frac{t}{0 . 02} \right) \right\} \times \frac{1}{0 . 02}\]
\[ \Rightarrow \nu = - 0 . 50 \cos 2\pi \left\{ \left( \frac{x}{4} \right) - \left( \frac{t}{0 . 02} \right) \right\}\]
\[At x = 1 \text{ and } t = 0 . 01 s, \nu = - 0 . 50 \cos 2\pi \left\{ \frac{1}{4} - \frac{1}{2} \right\} = 0 .\]
(c) (i) Speed of the particle:
\[At x = 3 cm \text{ and } t = 0 . 01 s,\]
\[\nu = - 0 . 50\cos2\pi\left\{ \frac{3}{4} - \frac{1}{2} \right\} = 0\]
(ii) \[\text{ At } x = 5 cm \text{ and } t = 0 . 01 s,\]
\[\nu = 0 \]
\[\left( iii \right) At x = 7 cm \text{ and } t = 0 . 1 s, \nu = 0 . \]
\[\]
\[\left( iv \right) At x = 1 cm \text{ and } t = 0 . 011 s, \]
\[\nu = 50 \cos 2\pi\left\{ \left( \frac{1}{4} \right) - \left( \frac{0 . 011}{0 . 02} \right) \right\}\]
\[ = - 50 \cos \left( \frac{3\pi}{5} \right) = - 9 . 7 cm/s\]
(By changing the value of t, the other two can be calculated.)
APPEARS IN
संबंधित प्रश्न
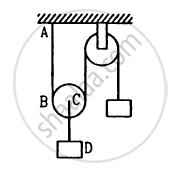
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
Choose the correct option:
A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
Change in temperature of the medium changes ______.
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
