Advertisements
Advertisements
प्रश्न
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
Advertisements
उत्तर
The wave equation is represented by \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right)\]
Let:
Time period = T
Wavelength = λ
\[\left( a \right) T = 2 \times 0 . 01 = 0 . 02 s = 20 ms\]
\[ \lambda = 2 \times 2 = 4 cm\]
(b) Equation for the velocity of the particle:
\[= - 0 . 50 \cos 2\pi\left\{ \left( \frac{x}{4} \right) - \left( \frac{t}{0 . 02} \right) \right\} \times \frac{1}{0 . 02}\]
\[ \Rightarrow \nu = - 0 . 50 \cos 2\pi \left\{ \left( \frac{x}{4} \right) - \left( \frac{t}{0 . 02} \right) \right\}\]
\[At x = 1 \text{ and } t = 0 . 01 s, \nu = - 0 . 50 \cos 2\pi \left\{ \frac{1}{4} - \frac{1}{2} \right\} = 0 .\]
(c) (i) Speed of the particle:
\[At x = 3 cm \text{ and } t = 0 . 01 s,\]
\[\nu = - 0 . 50\cos2\pi\left\{ \frac{3}{4} - \frac{1}{2} \right\} = 0\]
(ii) \[\text{ At } x = 5 cm \text{ and } t = 0 . 01 s,\]
\[\nu = 0 \]
\[\left( iii \right) At x = 7 cm \text{ and } t = 0 . 1 s, \nu = 0 . \]
\[\]
\[\left( iv \right) At x = 1 cm \text{ and } t = 0 . 011 s, \]
\[\nu = 50 \cos 2\pi\left\{ \left( \frac{1}{4} \right) - \left( \frac{0 . 011}{0 . 02} \right) \right\}\]
\[ = - 50 \cos \left( \frac{3\pi}{5} \right) = - 9 . 7 cm/s\]
(By changing the value of t, the other two can be calculated.)
APPEARS IN
संबंधित प्रश्न
Which of the following is a mechanical wave?
A cork floating in a calm pond executes simple harmonic motion of frequency
\[\nu\] when a wave generated by a boat passes by it. The frequency of the wave is
The fundamental frequency of a string is proportional to
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
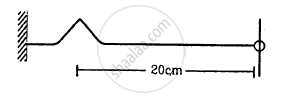
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
