Advertisements
Advertisements
प्रश्न
A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
उत्तर
Given:
Speed of sound in air v = 332 ms−1
Radius of the circle r = \[\frac{100}{\pi}\] cm =\[\frac{1}{\pi}\] m
Frequency of sound of the source \[f_0\]= 500 Hz
Angular speed \[\omega\]= 5 rev/s
Linear speed of the source is given by:
\[v = \omega r\]
⇒ \[v = 5 \times \frac{1}{\pi} = \frac{5}{\pi} = 1 . 59 \text { m/s }\]
∴ velocity of source \[v_s\]= 1.59 m/s
Let X be the position where the observer will listen at a maximum and Y be the position where he will listen at the minimum frequency.
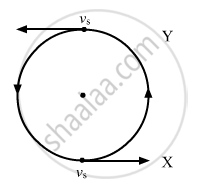
Apparent frequency \[\left( f_1 \right)\]at X is given by :
\[f_1 = \left( \frac{v}{v - v_s} \right) f_0\]
On substituting the values in the above equation, we get:
\[f_1 = \left( \frac{332}{332 - 1 . 59} \right) \times 500 \approx 515 \text { Hz }\]
Apparent frequency \[\left( f_2 \right)\] at Y is given by:
\[f_2 = \left( \frac{v}{v + v_s} \right) f_0\]
On substituting the values in the above equation, we get:
APPEARS IN
संबंधित प्रश्न
A cork floating in a calm pond executes simple harmonic motion of frequency
\[\nu\] when a wave generated by a boat passes by it. The frequency of the wave is
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
The fundamental frequency of a string is proportional to
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
Two tuning forks having frequencies 320 Hz and 340 Hz are sounded together to produce sound waves. The velocity of sound in air is 340 m/s. Find the difference in wavelength of these waves.
