Advertisements
Advertisements
प्रश्न
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
उत्तर
For source A :
Wavelength \[\lambda\] = 32 cm = 32\[\times\]`10^\{-}`2 m
Velocity v = 350 `ms^(-1)`
Frequency \[\left( n_1 \right)\] is given by :
\[ n_1 = \frac{v}{\lambda} = \frac{350}{32 \times {10}^{- 2}} = 1093 . 75 \text { Hz }\]
For source B:
Velocity v = 350 ms−1
Wavelength \[\lambda\] = 32.2 cm = 32.2\[\times\] `10^\(-)`2 m
Frequency \[\left( n_2 \right)\] is given by :
\[ n_2 = \frac{v}{\lambda} = \frac{350}{32 . 2 \times {10}^{- 2}} = 1086 . 96 \text { Hz }\]
∴ Beat frequency = 1093.75 − 1086.96 = 6.79 Hz \[\approx\] 7 Hz
APPEARS IN
संबंधित प्रश्न
A cork floating in a calm pond executes simple harmonic motion of frequency
\[\nu\] when a wave generated by a boat passes by it. The frequency of the wave is
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
The fundamental frequency of a string is proportional to
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
In a stationary wave,
(a) all the particles of the medium vibrate in phase
(b) all the antinodes vibrates in phase
(c) the alternate antinodes vibrate in phase
(d) all the particles between consecutive nodes vibrate in phase.
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
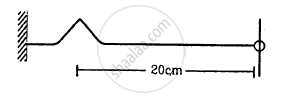
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
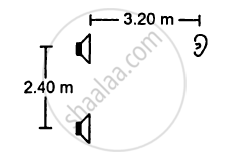
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
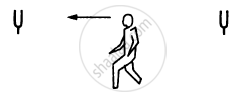
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
