Advertisements
Advertisements
प्रश्न
Two identical tuning forks vibrating at the same frequency 256 Hz are kept fixed at some distance apart. A listener runs between the forks at a speed of 3.0m s−1 so that he approaches one tuning fork and recedes from the other figure. Find the beat frequency observed by the listener. Speed of sound in air = 332 m s−1.
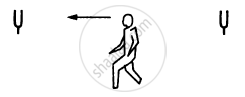
उत्तर
Given:
Speed of sound in air v = 332 ms−1
Velocity of the observer \[v_0\]= 3 `\text {ms}^\(-)`1
Velocity of the source \[v_s\]= 0
Frequency of the tuning forks \[f_0\]= 256 Hz
The apparent frequency\[\left( f_1 \right)\] heard by the man when he is running towards the tuning forks is \[f_1 = \left( \frac{v + v_0}{v} \right) \times f_0\]
On substituting the values in the above equation, we get:
\[f_1 = \left( \frac{332 + 3}{332} \right) \times 256 = 258 . 3 \text { Hz }\]
The apparent frequency \[\left( f_2 \right)\] heard by the man when he is running away from the tuning forks is \[f_2 = \left( \frac{v - v_0}{v} \right) \times f_0\]
On substituting the values in the above equation, we get :
\[f_2 = \left( \frac{332 - 3}{332} \right) \times 256\]
\[ = 253 . 7 \text { Hz }.\]
∴ beats produced by them
=\[f_2 - f_1\]
=258.3 − 253.7 = 4.6 Hz
APPEARS IN
संबंधित प्रश्न
Which of the following is a mechanical wave?
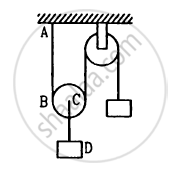
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
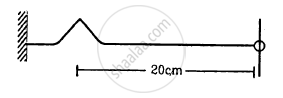
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
