Advertisements
Advertisements
प्रश्न
Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
उत्तर
Given:
Speed of sound in air v = 340 m/s
Length of open organ pipe L = 20 cm = 20 × 10−2 m
Fundamental frequency \[\left( f \right)\] of an open organ pipe :
\[f = \left( \frac{v}{2L} \right) = \frac{340}{2 \times 20 \times {10}^{- 2}}=850\text { Hz }\]
First overtone frequency \[\left( f_1 \right)\] :
f1 = \[2f\]
\[\Rightarrow f_1 = \left( \frac{2V}{2I} \right) = 2 \times 850 = 1700 \text{ Hz }\]
Second overtone frequency \[\left( f_2 \right)\] :
\[f_2 = 3f\]\[ \Rightarrow f_2 = 3\left( \frac{V}{2L} \right) = 3 \times 850 = 2550 \text { Hz }\]
APPEARS IN
संबंधित प्रश्न
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
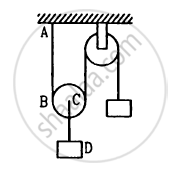
The fundamental frequency of a string is proportional to
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
A bat emitting an ultrasonic wave of frequency 4.5 × 104 Hz flies at a speed of 6 m s−1between two parallel walls. Find the fractional heard by the bat and the beat frequencies heard by the bat and the beat frequency between the two. The speed of sound is 330 m s−1.
A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
