Advertisements
Advertisements
प्रश्न
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
उत्तर
(c) Frequency = 25/π Hz
(d) Amplitude = 0⋅001 mm
\[y = \left( 0 \cdot 001 mm \right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
Equating the above equation with the general equation, we get:
\[y = A\sin\left( \omega t - kx \right)\]
\[\omega = \frac{2\pi}{T} = 2\pi v\]
\[k = \frac{2\pi}{\lambda}\]
Here, A is the amplitude, ω is the angular frequency, k is the wave number and λ is the wavelength.
\[A = 0 . 001 mm\]
\[Now, \]
\[50 = 2\pi\nu\]
\[ \Rightarrow \nu = \frac{25}{\pi} Hz\]
APPEARS IN
संबंधित प्रश्न
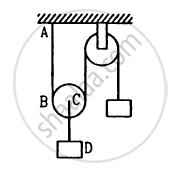
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
Choose the correct option:
A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
A piano wire weighing 6⋅00 g and having a length of 90⋅0 cm emits a fundamental frequency corresponding to the "Middle C" \[\left( \nu = 261 \cdot 63 Hz \right)\]. Find the tension in the wire.
In Quincke's experiment, the sound intensity has a minimum value l at a particular position. As the sliding tube is pulled out by a distance of 16.5 mm, the intensity increases to a maximum of 9 l. Take the speed of sound in air to be 330 m s−1. (a) Find the frequency of the sound source. (b) Find the ratio of the amplitudes of the two waves arriving at the detector assuming that it does not change much between the positions of minimum intensity and maximum intensity.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
The horn of a car emits sound with a dominant frequency of 2400 Hz. What will be the apparent dominant frequency heard by a person standing on the road in front of the car if the car is approaching at 18.0 km h−1? Speed of sound in air = 340 m s−1.
A person riding a car moving at 72 km h−1 sound a whistle emitting a wave of frequency 1250 Hz. What frequency will be heard by another person standing on the road (a) in front of the car (b) behind the car? Speed of sound in air = 340 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
