Advertisements
Advertisements
प्रश्न
Choose the correct option:
A standing wave is produced on a string clamped at one end and free at the other. The length of the string ______.
विकल्प
Must be an odd integral multiple of `lambda/4`
Must be an odd integral multiple of `lambda/2`
Must be an odd integral multiple of `lambda`
Must be an even integral multiple of `lambda`
उत्तर
A standing wave is produced on a string clamped at one end and free at the other. The length of the string must be an odd integral multiple of `lambda/4`.
Explanation:
The frequency (v) of a standing wave, fixed at one end and free at the other end is:
v = `((2n + 1)/2) v/(2L)`
Since V = `vlambda`
⇒ v = `(n + 1/2) (Vlambda)/(2L)`
⇒ L = `((2n + 1)/4)lambda`
⇒ L = `lambda/4, (3lambda)/4`,....
Therefore the length of the string is an odd integral multiple of `lambda/4`.
APPEARS IN
संबंधित प्रश्न
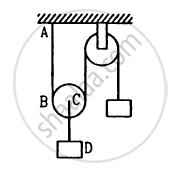
Both the strings, shown in figure, are made of same material and have same cross section. The pulleys are light. The wave speed of a transverse wave in the string AB is
\[\nu_1\] and in CD it is \[\nu_2\]. Then \[\nu_1 / \nu_2\]
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
The speed of sound in a medium depends on
Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
The speed of sound as measured by a student in the laboratory on a winter day is 340 m s−1 when the room temperature is C17°. What speed will be measured by another student repeating the experiment on a day when the room temperature is 32°C?
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
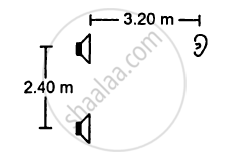
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
Find the fundamental, first overtone and second overtone frequencies of an open organ pipe of length 20 cm. Speed of sound in air is 340 ms−1.
A closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air = 340 m s−1.
A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8 km s−1.
Find the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20 − 20,000 Hz). Speed of sound in air = 340 m s−1.
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode. A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air = 340 m s−1.
A Kundt's tube apparatus has a copper rod of length 1.0 m clamped at 25 cm from one of the ends. The tube contains air in which the speed of sound is 340 m s−1. The powder collects in heaps separated by a distance of 5.0 cm. Find the speed of sound waves in copper.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
A tuning fork of unknown frequency makes 5 beats per second with another tuning fork which can cause a closed organ pipe of length 40 cm to vibrate in its fundamental mode. The beat frequency decreases when the first tuning fork is slightly loaded with wax. Find its original frequency. The speed of sound in air is 320 m s−1.
A person riding a car moving at 72 km h−1 sound a whistle emitting a wave of frequency 1250 Hz. What frequency will be heard by another person standing on the road (a) in front of the car (b) behind the car? Speed of sound in air = 340 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

A small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 100/π cm at a constant angular speed of 5.0 revolutions per second. A listener situation situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air = 332 m s−1.
A car moving at 108 km h−1 finds another car in front it going in the same direction at 72 km h−1. The first car sounds a horn that has a dominant frequency of 800 Hz. What will be the apparent frequency heard by the driver in the front car? Speed of sound in air = 330 m s−1.
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A wave of frequency 500 Hz is traveling with a speed of 350 m/s. (a) What is the phase difference between two displacements at a certain point at times 1.0 ms apart? (b) what will be the smallest distance between two points which are 45° out of phase at an instant of time?
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
The speed of sound in hydrogen is 1270 m/s. The speed of sound in the mixture of oxygen and hydrogen in which they are mixed in 1:4 ratio is
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
