Advertisements
Advertisements
प्रश्न
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

उत्तर
Given:
Frequency of tuning forks \[f_0\]= 512 Hz
Speed of sound in air v = 330 ms−1
Velocity of tuning forks \[v_s\]= 5.5 ms−1
The apparent frequency \[\left( f_1 \right)\] heard by the person from the tuning fork on the left is given by:
\[f_1 = \left( \frac{v}{v + v_s} \right) \times f_0\]
On substituting the values in the above equation, we get:
\[f_1 = \left( \frac{330}{330 + 55} \right) \times 512\]
\[ = 503 . 60 \text { Hz }\]
Similarly, apparent frequency \[\left( f_2 \right)\] heard by the person from the tuning fork on the right is given by:
\[f_2 = \left( \frac{v}{v - v_s} \right) \times f_0\]
On substituting the values in the above equation, we get:
\[f_2 = \left( \frac{330}{330 - 5 . 5} \right) \times 512\]
\[ = 520 . 68 \text { Hz }\]
∴ beats produced
=\[f_2 - f_1\]
= 520.68 − 503.60 = 17.5 Hz
As the difference is greater than 10 (the persistence of sound for the human ear is 1/10 of a second), the sound gets overlapped, and the observer cannot distinguish between the sounds and the beats.
APPEARS IN
संबंधित प्रश्न
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
Two periodic waves of amplitudes A1 and A2 pass thorough a region. If A1 > A2, the difference in the maximum and minimum resultant amplitude possible is
The fundamental frequency of a string is proportional to
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
Calculate the speed of sound in oxygen from the following data. The mass of 22.4 litre of oxygen at STP (T = 273 K and p = 1.0 × 105 N m−2) is 32 g, the molar heat capacity of oxygen at constant volume is Cv = 2.5 R and that at constant pressure is Cp = 3.5 R.
Find the change in the volume of 1.0 litre kerosene when it is subjected to an extra pressure of 2.0 × 105 N m−2 from the following data. Density of kerosene = 800 kg m−3and speed of sound in kerosene = 1330 ms−1.
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
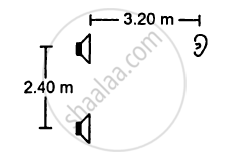
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air = 320 m s−1.
An electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air = 320 m s−1.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
A train approaching a platform at a speed of 54 km h−1 sounds a whistle. An observer on the platform finds its frequency to be 1620 Hz. the train passes the platform keeping the whistle on and without slowing down. What frequency will the observer hear after the train has crossed the platform? The speed of sound in air = 332 m s−1.
Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
Two submarines are approaching each other in a calm sea. The first submarine travels at a speed of 36 km h−1 and the other at 54 km h−1 relative to the water. The first submarine sends a sound signal (sound waves in water are also called sonar) at a frequency of 2000 Hz. (a) At what frequency is this signal received from the second submarine. At what frequency is this signal received by the first submarine. Take the speed of of the sound wave in water to be 1500 m s−1.
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
Two tuning forks having frequencies 320 Hz and 340 Hz are sounded together to produce sound waves. The velocity of sound in air is 340 m/s. Find the difference in wavelength of these waves.
