Advertisements
Advertisements
प्रश्न
A Kundt's tube apparatus has a steel rod of length 1.0 m clamped at the centre. It is vibrated in its fundamental mode at a frequency of 2600 Hz. The lycopodium powder dispersed in the tube collects into heaps separated by 6.5 cm. Calculate the speed of sound in steel and in air.
उत्तर
Given :
Length at which steel rod is clamped l = \[\frac{1}{2} = 0 . 5 \text { m }\]
Fundamental mode of frequency f = 2600 Hz
Distance between the two heaps \[∆ l\] = 6.5 cm = \[6 . 5 \times {10}^{- 2} \text { m }\]
Since Kundt's tube apparatus is a closed organ pipe, its fundamental frequency is given by :
\[f = \frac{v_{air}}{4L}\]
\[ \Rightarrow v_{air} = f \times 2 \times ∆ L\]
\[ \Rightarrow v_{air} = 2600 \times 2 \times 6 . 5 \times {10}^{- 2} = 338 \text { m/s }\]
\[(b) \frac{v_{steel}}{v_{air}} = \frac{2 \times l}{∆ l}\]
\[ \Rightarrow v_{steel} = \frac{2l}{∆ l} \times v_{air} \]
\[ \Rightarrow v_{steel} = \frac{2 \times 0 . 5 \times 338}{6 . 5 \times {10}^{- 2}}\]
\[ \Rightarrow v_{steel} = 5200 \text { m/s }\]
APPEARS IN
संबंधित प्रश्न
Which of the following is a mechanical wave?
Two particles A and B have a phase difference of π when a sine wave passes through the region.
(a) A oscillates at half the frequency of B.
(b) A and B move in opposite directions.
(c) A and B must be separated by half of the wavelength.
(d) The displacements at A and B have equal magnitudes.
In a stationary wave,
(a) all the particles of the medium vibrate in phase
(b) all the antinodes vibrates in phase
(c) the alternate antinodes vibrate in phase
(d) all the particles between consecutive nodes vibrate in phase.
A string of linear mass density 0⋅5 g cm−1 and a total length 30 cm is tied to a fixed wall at one end and to a frictionless ring at the other end (See figure). The ring can move on a vertical rod. A wave pulse is produced on the string which moves towards the ring at a speed of 20 cm s−1. The pulse is symmetric about its maximum which is located at a distance of 20 cm from the end joined to the ring. (a) Assuming that the wave is reflected from the ends without loss of energy, find the time taken by the string to region its shape. (b) The shape of the string changes periodically with time. Find this time period. (c) What is the tension in the string?
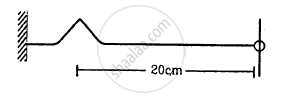
A one-metre long stretched string having a mass of 40 g is attached to a tuning fork. The fork vibrates at 128 Hz in a direction perpendicular to the string. What should be the tension in the string if it is to vibrate in four loops?
Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air = 320 m s−1.
In a resonance column experiment, a tuning fork of frequency 400 Hz is used. The first resonance is observed when the air column has a length of 20.0 cm and the second resonance is observed when the air column has a length of 62.0 cm. (a) Find the speed of sound in air. (b) How much distance above the open end does the pressure node form?
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
Two successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324 ms−1.
A person riding a car moving at 72 km h−1 sound a whistle emitting a wave of frequency 1250 Hz. What frequency will be heard by another person standing on the road (a) in front of the car (b) behind the car? Speed of sound in air = 340 m s−1.
A bullet passes past a person at a speed of 220 m s−1. Find the fractional change in the frequency of the whistling sound heard by the person as the bullet crosses the person. Speed of sound in air = 330 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
A source emitting sound at frequency 4000 Hz, is moving along the Y-axis with a speed of 22 m s−1. A listener is situated on the ground at the position (660 m, 0). Find the frequency of the sound received by the listener at the instant the source crosses the origin. Speed of sound in air = 330 m s−1.
A source emitting a sound of frequency v is placed at a large distance from an observer. The source starts moving towards the observer with a uniform acceleration a. Find the frequency heard by the observer corresponding to the wave emitted just after the source starts. The speed of sound in the medium is v.
The speed of a transverse wave in an elastic string is v0. If the tension in the string is reduced to half, then the speed of the wave is given by:
Two tuning forks having frequencies 320 Hz and 340 Hz are sounded together to produce sound waves. The velocity of sound in air is 340 m/s. Find the difference in wavelength of these waves.
