Advertisements
Advertisements
प्रश्न
A piston is fitted in a cylindrical tube of small cross section with the other end of the tube open. The tube resonates with a tuning fork of frequency 512 Hz. The piston is gradually pulled out of the tube and it is found that a second resonance occurs when the piston is pulled out through a distance of 32.0 cm. Calculate the speed of sound in the air of the tube.
उत्तर
Given:
Frequency of tuning fork f = 512 Hz
Let the speed of sound in the tube be v.
Let l1 be the length at which the piston resonates for the first time and l2 be the length at which the piston resonates for the second time.
We have:
l2 =2l1 = 2 \[\times\]32 = 64 cm =0.64 m
Velocity v = f \[\times\] l2
\[\Rightarrow\] v = 512 × 0.64 = 328 m/s
Hence, the speed of the sound in the tube is 328 m/s.
APPEARS IN
संबंधित प्रश्न
Two waves represented by \[y = a\sin\left( \omega t - kx \right)\] and \[y = a\cos\left( \omega t - kx \right)\] \[y = a\cos\left( \omega t - kx \right)\] are superposed. The resultant wave will have an amplitude
A wave pulse passing on a string with a speed of 40 cm s−1 in the negative x-direction has its maximum at x = 0 at t = 0. Where will this maximum be located at t = 5 s?
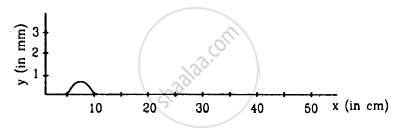
following Figure shows a wave pulse at t = 0. The pulse moves to the right with a speed of 10 cm s−1. Sketch the shape of the string at t = 1 s, 2 s and 3 s.
A wave is represented by the equation
\[y = \left( 0 \text{ cdot 001 mm }\right) \sin\left[ \left( 50 s^{- 1} \right)t + \left( 2 \cdot 0 m^{- 1} \right)x \right]\]
(a) The wave velocity = 100 m s−1.
(b) The wavelength = 2⋅0 m.
(c) The frequency = 25/π Hz.
(d) The amplitude = 0⋅001 mm.
A wave is described by the equation \[y = \left( 1 \cdot 0 mm \right) \sin \pi\left( \frac{x}{2 \cdot 0 cm} - \frac{t}{0 \cdot 01 s} \right) .\]
(a) Find the time period and the wavelength? (b) Write the equation for the velocity of the particles. Find the speed of the particle at x = 1⋅0 cm at time t = 0⋅01 s. (c) What are the speeds of the particles at x = 3⋅0 cm, 5⋅0 cm and 7⋅0 cm at t = 0⋅01 s?
(d) What are the speeds of the particles at x = 1⋅0 cm at t = 0⋅011, 0⋅012, and 0⋅013 s?
At a prayer meeting, the disciples sing JAI-RAM JAI-RAM. The sound amplified by a loudspeaker comes back after reflection from a building at a distance of 80 m from the meeting. What maximum time interval can be kept between one JAI-RAM and the next JAI-RAM so that the echo does not disturb a listener sitting in the meeting. Speed of sound in air is 320 m s−1.
In Quincke's experiment the sound detected is changed from a maximum to a minimum when the sliding tube is moved through a distance of 2.50 cm. Find the frequency of sound if the speed of sound in air is 340 m s−1.
An open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range? Speed of sound in air is 340 m s−1 and the audible range is 20-20,000 Hz.
A U-tube having unequal arm-lengths has water in it. A tuning fork of frequency 440 Hz can set up the air in the shorter arm in its fundamental mode of vibration and the same tuning fork can set up the air in the longer arm in its first overtone vibration. Find the length of the air columns. Neglect any end effect and assume that the speed of sound in air = 330 m s−1.
Calculate the frequency of beats produced in air when two sources of sound are activated, one emitting a wavelength of 32 cm and the other of 32.2 cm. The speed of sound in air is 350 m s−1.
Figure shows a person standing somewhere in between two identical tuning forks. each vibrating at 512 Hz. If both the tuning forks move towards right a speed of 5.5 m s−1, find the number of beats heard by the listener. Speed of sound in air = 330 m s−1.

Two trains are travelling towards each other both at a speed of 90 km h−1. If one of the trains sounds a whistle at 500 Hz, what will be the apparent frequency heard in the other train? Speed of sound in air = 350 m s−1.
A traffic policeman sounds a whistle to stop a car-driver approaching towards him. The car-driver does not stop and takes the plea in court that because of the Doppler shift, the frequency of the whistle reaching him might have gone beyond the audible limit of 25 kHz and he did not hear it. Experiments showed that the whistle emits a sound with frequency closed to 16 kHz. Assuming that the claim of the driver is true, how fast was he driving the car? Take the speed of sound in air to be 330 m s−1. Is this speed practical with today's technology?
Two sources of sound are separated by a distance of 4 m. They both emit sound with the same amplitude and frequency (330 Hz), but they are 180° out of phase. At what points between the two sources, will the sound intensity be maximum?
A metallic wire of 1 m length has a mass of 10 × 10−3 kg. If the tension of 100 N is applied to a wire, what is the speed of the transverse wave?
A spring breaks under tension of 10 kg wt.If the string is used to revolve a body of mass 1.2 kg in a horizontal circle. of radius 50 cm, what is the maximum speed with which a body can be revolved?
