Advertisements
Advertisements
प्रश्न
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
Advertisements
उत्तर १
No, the converse is not true. The basic requirement for a wave function to represent a travelling wave is that for all values of x and t, wave function must have a finite value. Out of the given functions for y none satisfies this condition. Therefore, none can represent a travelling wave
उत्तर २
No;
(a) Does not represent a wave
(b) Represents a wave
(c) Does not represent a wave
The converse of the given statement is not true. The essential requirement for a function to represent a travelling wave is that it should remain finite for all values of x and t.
Explanation:
a) For x = 0 and t = 0, the function (x – vt)2 becomes 0.
Hence, for x = 0 and t = 0, the function represents a point and not a wave.
b) For x = 0 and t = 0, the function
`log ((x+vt)/x_0) = log 0 = prop`
Since the function does not converge to a finite value for x = 0 and t = 0, it represents a travelling wave
(c) For x = 0 and t = 0, the function
`1/(x + vt) = 1/0 = prop`
Since the function does not converge to a finite value for x = 0 and t = 0, it does not represent a travelling wave.
संबंधित प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `(3λ)/4`.
A wire stretched between two rigid supports vibrates in its fundamental mode with a frequency of 45 Hz. The mass of the wire is 3.5 × 10–2 kg and its linear mass density is 4.0 × 10–2 kg m–1. What is (a) the speed of a transverse wave on the string, and (b) the tension in the string?
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
Two waves of equal amplitude A, and equal frequency travel in the same direction in a medium. The amplitude of the resultant wave is
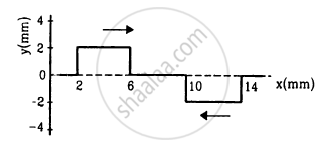
Following figure shows two wave pulses at t = 0 travelling on a string in opposite directions with the same wave speed 50 cm s−1. Sketch the shape of the string at t = 4 ms, 6 ms, 8 ms, and 12 ms.
A 2⋅00 m-long rope, having a mass of 80 g, is fixed at one end and is tied to a light string at the other end. The tension in the string is 256 N. (a) Find the frequencies of the fundamental and the first two overtones. (b) Find the wavelength in the fundamental and the first two overtones.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of `λ/2`.
Speed of sound wave in air ______.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
A steel wire has a length of 12 m and a mass of 2.10 kg. What will be the speed of a transverse wave on this wire when a tension of 2.06 × 104N is applied?
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
