Advertisements
Advertisements
प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with humidity.
उत्तर १
Let `"v"_"m" and "v"_"d"` be the speeds of sound in moist air and dry air respectively.
Let `rho_"m"` and `rho_"d"` be the densities of moist air and dry air respectively.
Take the relation:
`"v" = sqrt((gamma "P")/rho)`
Hence, the speed of sound in moist air is:
`"v"_"m" = sqrt((gamma "P")/rho_"m")` ....(i)
And the speed of sound in dry air is:
`"v"_"d" = sqrt((gamma "P")/rho_"d")` ...(ii)
On dividing equations (i) and (ii), we get:
`"v"_"m"/"v"_"d" = sqrt((gamma"P")/rho_"m" xx rho_"d"/(gamma"P")) = sqrt(rho_"d"/rho_"m")`
However, the presence of water vapour reduces the density of air, i.e.,
`rho_"d" < rho_"m"`
`:. v_"m" > v_"d"`
Hence, the speed of sound in moist air is greater than it is in dry air. Thus, in a gaseous medium, the speed of sound increases with humidity.
उत्तर २
We are given that `"v" = sqrt((gamma "p")/rho)`
We know PV = nRT (For n moles of ideal gas)
`=> "PV" = "m"/"M" "RT"`
where m is the total mass and M is the molecular mass of the gas
`:. "P" = "m"/"M" * "RT"/"M" = (rho "RT")/"M"`
`=> "P"/rho = "RT"/"M"`
Increase in humidity decrease the effective density of air. Therefore the velocity `("v" prop 1/sqrtrho)` increase.
APPEARS IN
संबंधित प्रश्न
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
Velocity of sound in air is 332 m s−1. Its velocity in vacuum will be
Two wires A and B, having identical geometrical construction, are stretched from their natural length by small but equal amount. The Young modules of the wires are YA and YB whereas the densities are \[\rho_A \text{ and } \rho_B\]. It is given that YA > YB and \[\rho_A > \rho_B\]. A transverse signal started at one end takes a time t1 to reach the other end for A and t2 for B.
A pulse travelling on a string is represented by the function \[y = \frac{a^2}{\left( x - \nu t \right)^2 + a^2},\] where a = 5 mm and ν = 20 cm-1. Sketch the shape of the string at t = 0, 1 s and 2 s. Take x = 0 in the middle of the string.
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
The equation for the vibration of a string, fixed at both ends vibrating in its third harmonic, is given by
\[y = \left( 0 \cdot 4 cm \right) \sin\left[ \left( 0 \cdot 314 {cm}^{- 1} \right) x \right] \cos \left[ \left( 600\pi s^{- 1} \right) t \right]\]
(a) What is the frequency of vibration? (b) What are the positions of the nodes? (c) What is the length of the string? (d) What is the wavelength and the speed of two travelling waves that can interfere to give this vibration?
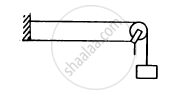
Following figure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning for. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the the reflected sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
