Advertisements
Advertisements
प्रश्न
A 200 Hz wave with amplitude 1 mm travels on a long string of linear mass density 6 g m−1 kept under a tension of 60 N. (a) Find the average power transmitted across a given point on the string. (b) Find the total energy associated with the wave in a 2⋅0 m long portion of the string.
उत्तर
Given,
Frequency of the wave, f = 200 Hz
Amplitude, A = 1 mm = 10−3 m
Linear mass density, m = 6 gm−3
Applied tension, T = 60 N
Now,
Let the velocity of the wave be v.
Thus, we have:
\[v = \sqrt{\left( \frac{T}{m} \right)} = \sqrt{\frac{\left( 60 \right)}{\left( 6 \times {10}^{- 3} \right)}}\]
\[ = {10}^2 = 100 m/s\]
(a) Average power is given as
\[P_{average} = 2 \pi^2 m\nu A^2 f^2 \]
\[= 2 \times \left( 3 . 14 \right)^2 \times \left( 6 \times {10}^{- 3} \right) \times 100 \times \left( {10}^{- 3} \right) \times {200}^2 \]
\[ = 473 \times {10}^{- 3} = 0 . 47 W\]
(b) Length of the string = 2 m
Time required to cover this distance:
\[t = \frac{2}{100} = 0 . 02 s\]
\[Energy = Power \times t\]
\[ = 0 . 47 \times 0 . 02\]
\[ = 9 . 4 \times {10}^{- 3} J = 9 . 4 mJ\]
APPEARS IN
संबंधित प्रश्न
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
Show that the particle speed can never be equal to the wave speed in a sine wave if the amplitude is less than wavelength divided by 2π.
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
Two sine waves travel in the same direction in a medium. The amplitude of each wave is A and the phase difference between the two waves is 120°. The resultant amplitude will be
The equation of a wave travelling on a string stretched along the X-axis is given by
\[y = A e {}^- \left( \frac{x}{a} + \frac{t}{T} \right)^2 .\]
(a) Write the dimensions of A, a and T. (b) Find the wave speed. (c) In which direction is the wave travelling? (d) Where is the maximum of the pulse located at t = T? At t = 2 T?
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
The displacement of the particle at x = 0 of a stretched string carrying a wave in the positive x-direction is given f(t) = A sin (t/T). The wave speed is v. Write the wave equation.
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
The equation of a wave travelling on a string is \[y = \left( 0 \cdot 10 \text{ mm } \right) \sin\left[ \left( 31 \cdot 4 m^{- 1} \right)x + \left( 314 s^{- 1} \right)t \right]\]
(a) In which direction does the wave travel? (b) Find the wave speed, the wavelength and the frequency of the wave. (c) What is the maximum displacement and the maximum speed of a portion of the string?
A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1⋅0 and the displacement becomes zero 200 times per second. The linear mass density of the string is 0⋅10 kg m−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
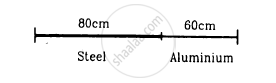
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
An organ pipe of length 0.4 m is open at both ends. The speed of sound in the air is 340 m/s. The fundamental frequency is ______
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
For the travelling harmonic wave
y (x, t) = 2.0 cos 2π (10t – 0.0080x + 0.35)
Where x and y are in cm and t in s. Calculate the phase difference between oscillatory motion of two points separated by a distance of 4 m.
A string of mass 2.5 kg is under a tension of 200 N. The length of the stretched string is 20.0 m. If the transverse jerk is struck at one end of the string, the disturbance will reach the other end in ______.
If c is r.m.s. speed of molecules in a gas and v is the speed of sound waves in the gas, show that c/v is constant and independent of temperature for all diatomic gases.
An engine is approaching a cliff at a constant speed. When it is at a distance of 0.9 km from cliff it sounds a whistle. The echo of the sound is heard by the driver after 5 seconds. Velocity of sound in air is equal to 330 ms-1. The speed of the engine is ______ km/h.
