Advertisements
Advertisements
प्रश्न
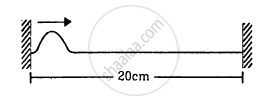
A string of length 20 cm and linear mass density 0⋅40 g cm−1 is fixed at both ends and is kept under a tension of 16 N. A wave pulse is produced at t = 0 near an ends as shown in the figure, which travels towards the other end. (a) When will the string have the shape shown in the figure again? (b) Sketch the shape of the string at a time half of that found in part (a).
उत्तर
Given,
Length of the string = 20 cm
Linear mass density of the string = 0.40 g cm−1
Applied tension = 16 N = \[16 \times {10}^5 dyn\]
Velocity of the wave:
\[\nu = \sqrt{\left( \frac{T}{m} \right)}\]
\[ = \sqrt{\frac{\left( 16 \times {10}^5 \right)}{0 . 4}}\]
\[ = 2000 \text{ cm }/s\]
∴ Time taken to reach the other end
\[= \frac{20}{2000} = 0 . 01 s\]
Time taken to see the pulse again in the original position
\[= 0 . 01 \times 2 = 0 . 02 s\]
(b) At t = 0.01 s, there will be a trough at the right end as it is reflected.
APPEARS IN
संबंधित प्रश्न
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top given that the speed of sound in air is 340 m s–1? (g= 9.8 m s–2)
A steel wire has a length of 12.0 m and a mass of 2.10 kg. What should be the tension in the wire so that speed of a transverse wave on the wire equals the speed of sound in dry air at 20 °C = 343 m s–1.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the transmitted sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A hospital uses an ultrasonic scanner to locate tumours in a tissue. What is the wavelength of sound in the tissue in which the speed of sound is 1.7 km s–1? The operating frequency of the scanner is 4.2 MHz.
A metre-long tube open at one end, with a movable piston at the other end, shows resonance with a fixed frequency source (a tuning fork of frequency 340 Hz) when the tube length is 25.5 cm or 79.3 cm. Estimate the speed of sound in air at the temperature of the experiment. The edge effects may be neglected.
A steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53 kHz. What is the speed of sound in steel?
A train, standing in a station-yard, blows a whistle of frequency 400 Hz in still air. The wind starts blowing in the direction from the yard to the station with at a speed of 10 m s–1. What are the frequency, wavelength, and speed of sound for an observer standing on the station’s platform? Is the situation exactly identical to the case when the air is still and the observer runs towards the yard at a speed of 10 m s–1? The speed of sound in still air can be taken as 340 m s–1.
A SONAR system fixed in a submarine operates at a frequency 40.0 kHz. An enemy submarine moves towards the SONAR with a speed of 360 km h–1. What is the frequency of sound reflected by the submarine? Take the speed of sound in water to be 1450 m s–1.
Show that for a wave travelling on a string
\[\frac{y_{max}}{\nu_{max}} = \frac{\nu_{max}}{\alpha_{max}},\]
where the symbols have usual meanings. Can we use componendo and dividendo taught in algebra to write
\[\frac{y_{max} + \nu_{max}}{\nu_{max} - \nu_{max}} = \frac{\nu_{max} + \alpha_{max}}{\nu_{max} - \alpha_{max}}?\]
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
A wave pulse is travelling on a string with a speed \[\nu\] towards the positive X-axis. The shape of the string at t = 0 is given by g(x) = Asin(x/a), where A and a are constants. (a) What are the dimensions of A and a ? (b) Write the equation of the wave for a general time t, if the wave speed is \[\nu\].
A travelling wave is produced on a long horizontal string by vibrating an end up and down sinusoidally. The amplitude of vibration is 1⋅0 and the displacement becomes zero 200 times per second. The linear mass density of the string is 0⋅10 kg m−1 and it is kept under a tension of 90 N. (a) Find the speed and the wavelength of the wave. (b) Assume that the wave moves in the positive x-direction and at t = 0, the end x = 0 is at its positive extreme position. Write the wave equation. (c) Find the velocity and acceleration of the particle at x = 50 cm at time t = 10 ms.
A steel wire fixed at both ends has a fundamental frequency of 200 Hz. A person can hear sound of maximum frequency 14 kHz. What is the highest harmonic that can be played on this string which is audible to the person?
What is the interference of sound waves?
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air is independent of pressure.
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air increases with temperature.
A bat emits an ultrasonic sound of frequency 1000 kHz in the air. If the sound meets a water surface, what is the wavelength of the the reflected sound? The speed of sound in air is 340 m s–1 and in water 1486 m s–1.
A sound wave is passing through air column in the form of compression and rarefaction. In consecutive compressions and rarefactions ______.
The amplitude of wave disturbance propagating in the positive x-direction given is by `1/(1 + x)^2` at time t = 0 and `1/(1 + (x - 2)^2)` at t = 1 s, where x and y are in 2 metres. The shape of wave does not change during the propagation. The velocity of the wave will be ______ m/s.
Two perfectly identical wires kept under tension are in unison. When the tension in the wire is increased by 1% then on sounding them together 3 beats are heard in 2 seconds. What is the frequency of each wire?
