Advertisements
Advertisements
प्रश्न
A steel wire of length 64 cm weighs 5 g. If it is stretched by a force of 8 N, what would be the speed of a transverse wave passing on it?
उत्तर
Given,
Length of the steel wire = 64 cm
Weight = 5 g
Applied force = 8 N
Thus, we have:
\[\text{ Mass per unit length = \frac{5}{64} gm/cm}\]
\[Tension, T = 8 N\]
\[ = 8 \times {10}^5 dyn\]
\[Speed, v = \sqrt{\left( \frac{T}{m} \right)}\]
\[ = \sqrt{\frac{\left( 8 \times {10}^5 \times 64 \right)}{5}}\]
\[ = 3200 \text{ cm/s = 32 m/s }\]
APPEARS IN
संबंधित प्रश्न
A wire of density ‘ρ’ and Young’s modulus ‘Y’ is stretched between two rigid supports separated by a distance ‘L’ under tension ‘T’. Derive an expression for its frequency in fundamental mode. Hence show that `n=1/(2L)sqrt((Yl)/(rhoL))` where symbols have their usual meanings
Explain why (or how): Bats can ascertain distances, directions, nature, and sizes of the obstacles without any “eyes”,
Longitudinal waves cannot
A wave going in a solid
(a) must be longitudinal
(b) may be longitudinal
(c) must be transverse
(d) may be transverse.
A wave moving in a gas
Mark out the correct options.
A particle on a stretched string supporting a travelling wave, takes 5⋅0 ms to move from its mean position to the extreme position. The distance between two consecutive particles, which are at their mean positions, is 2⋅0 cm. Find the frequency, the wavelength and the wave speed.
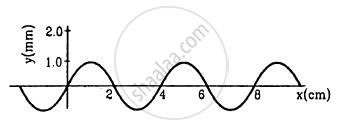
Figure shows a plot of the transverse displacements of the particles of a string at t = 0 through which a travelling wave is passing in the positive x-direction. The wave speed is 20 cm s−1. Find (a) the amplitude, (b) the wavelength, (c) the wave number and (d) the frequency of the wave.
Two wires of different densities but same area of cross section are soldered together at one end and are stretched to a tension T. The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
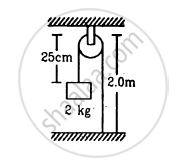
In the arrangement shown in figure , the string has a mass of 4⋅5 g. How much time will it take for a transverse disturbance produced at the floor to reach the pulley? Take g = 10 m s−2.
A heavy but uniform rope of length L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach the ceiling? (c) A particle is dropped from the ceiling at the instant the bottom end is given the jerk. Where will the particle meet the pulse?
A tuning fork of frequency 440 Hz is attached to a long string of linear mass density 0⋅01 kg m−1 kept under a tension of 49 N. The fork produces transverse waves of amplitude 0⋅50 mm on the string. (a) Find the wave speed and the wavelength of the waves. (b) Find the maximum speed and acceleration of a particle of the string. (c) At what average rate is the tuning fork transmitting energy to the string?
A wire, fixed at both ends is seen to vibrate at a resonant frequency of 240 Hz and also at 320 Hz. (a) What could be the maximum value of the fundamental frequency? (b) If transverse waves can travel on this string at a speed of 40 m s−1, what is its length?
A 660 Hz tuning fork sets up vibration in a string clamped at both ends. The wave speed for a transverse wave on this string is 220 m s−1 and the string vibrates in three loops. (a) Find the length of the string. (b) If the maximum amplitude of a particle is 0⋅5 cm, write a suitable equation describing the motion.
Three resonant frequencies of a string are 90, 150 and 210 Hz. (a) Find the highest possible fundamental frequency of vibration of this string. (b) Which harmonics of the fundamental are the given frequencies? (c) Which overtones are these frequencies? (d) If the length of the string is 80 cm, what would be the speed of a transverse wave on this string?
The phenomenon of beats can take place
