Advertisements
Advertisements
प्रश्न
Use the formula `v = sqrt((gamma P)/rho)` to explain why the speed of sound in air is independent of pressure.
उत्तर १
Take the relation:
`v = sqrt((gamma P)/rho)` ....(i)
where
Density, `rho = "Mass"/"Volume" = M/V`
M = Molecular weight of the gas
V = Volume of the gas
Hence, equation (i) reduces to
`v = sqrt((gamma "PV")/"M")` .....(ii)
Now from the ideal gas equation for n = 1:
PV = RT
For constant T, PV = Constant
Since both M and γ are constants, v = Constant
Hence, at a constant temperature, the speed of sound in a gaseous medium is independent of the change in the pressure of the gas.
उत्तर २
We are given that `v = sqrt((gamma p)/rho)`
We know PV = nRT (For n moles of ideal gas)
`=> "PV" = "m"/"M" "RT"`
where m is the total mass and M is the molecular mass of the gas
`:. P = "m"/"M" * "RT"/"M"`
`= (rho"RT")/"M"`
`=> "P"/rho = "RT"/"M"`
For a gas at constant temperature `"P"/rho = "constant"`
∴ As P increase, rho also increase and vice versa. This implies that `v = sqrt((gamma P)/rho)` = constant, i.e velocity is independent of pressure of the gas.
APPEARS IN
संबंधित प्रश्न
You have learnt that a travelling wave in one dimension is represented by a function y= f (x, t)where x and t must appear in the combination x – v t or x + v t, i.e. y = f (x ± v t). Is the converse true? Examine if the following functions for y can possibly represent a travelling wave:
(a) `(x – vt )^2`
(b) `log [(x + vt)/x_0]`
(c) `1/(x + vt)`
The radio and TV programmes, telecast at the studio, reach our antenna by wave motion. Is it a mechanical wave or nonmechanical?
Two strings A and B, made of same material, are stretched by same tension. The radius of string A is double of the radius of B. A transverse wave travels on A with speed `v_A` and on B with speed `v_B`. The ratio `v_A/v_B` is ______.
A wave pulse, travelling on a two-piece string, gets partially reflected and partially transmitted at the junction. The reflected wave is inverted in shape as compared to the incident one. If the incident wave has wavelength λ and the transmitted wave λ'
Two wave pulses travel in opposite directions on a string and approach each other. The shape of one pulse is inverted with respect to the other.
A sonometer wire of length l vibrates in fundamental mode when excited by a tuning fork of frequency 416. Hz. If the length is doubled keeping other things same, the string will ______.
A wave propagates on a string in the positive x-direction at a velocity \[\nu\] \[t = t_0\] is given by \[g\left( x, t_0 \right) = A \sin \left( x/a \right)\]. Write the wave equation for a general time t.
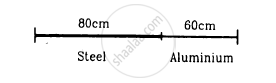
Figure shows an aluminium wire of length 60 cm joined to a steel wire of length 80 cm and stretched between two fixed supports. The tension produced is 40 N. The cross-sectional area of the steel wire is 1⋅0 mm2 and that of the aluminium wire is 3⋅0 mm2. What could be the minimum frequency of a tuning fork which can produce standing waves in the system with the joint as a node? The density of aluminium is 2⋅6 g cm−3 and that of steel is 7⋅8 g cm−3.
The string of a guitar is 80 cm long and has a fundamental frequency of 112 Hz. If a guitarist wishes to produce a frequency of 160 Hz, where should the person press the string?
Speed of sound waves in a fluid depends upon ______.
- directty on density of the medium.
- square of Bulk modulus of the medium.
- inversly on the square root of density.
- directly on the square root of bulk modulus of the medium.
