Advertisements
Advertisements
प्रश्न
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of Rs. 22 per litre which the container can hold.
उत्तर
Given that, height of milk container (h) = 16 cm,
Radius of lower end of milk container (r) = 8 cm
And radius of upper end of milk container (R) = 20 cm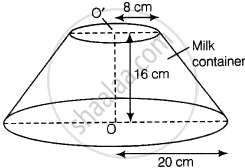
∴ Volume of the milk container made of metal sheet in the form of a frustum of a cone
= `(pih)/3 (R^2 + r^2 + Rr)`
= `22/7 xx 16/3 [(20)^2 + (8)^2 + 20 xx 8]`
= `(22 xx 16)/21 (400 + 64 + 160)`
= `(22 xx 16 xx 624)/21`
= `219648/21`
= 10459.42 cm3 ...[∵ 1L = 1000 cm3]
= 10.4592 L
So, volume of the milk container is 10459.42 cm3
∵ Cost of 1 L milk = ₹ 22
∴ Cost of 10.45942 L milk = 22 × 10.45942 = ₹ 230.12
Hence, the required cost of milk is ₹ 230.12
APPEARS IN
संबंधित प्रश्न
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of Rs 25 per metre ?\[[Use \pi = \frac{22}{7}]\]
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum?
A cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
A metalic solid cone is melted to form a solid cylinder of equal radius. If the height of the cylinder is 6 cm, then the height of the cone was
A spherical cannon ball, 28 cm in diameter, is melted and recast into a right circular conical mould with base diameter of 35 cm. Find the height of the cone.
A container, open at the top and made up of metal sheet, is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm, respectively. Find the cost of metal sheet used to make the container, if it costs ₹10 per 100 cm2
A cone is cut by a plane parallel to its base and the upper part is removed. The part that is left is called

The base radii of two circular cones of the same height are in the ratio 3 : 5. The ratio of their volumes are ______.
The shape of a glass (tumbler) (see figure) is usually in the form of ______.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form a cone of base diameter 8 cm. The height of the cone is ______.
