Advertisements
Advertisements
प्रश्न
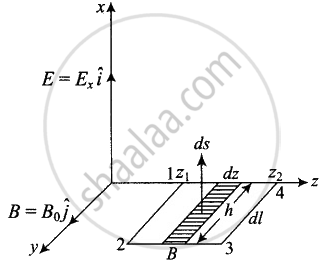
A plane EM wave travelling in vacuum along z direction is given by `E = E_0 sin(kz - ωt)hati` and `B = B_0 sin(kz - ωt)hatj`
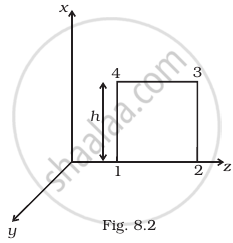
- Evaluate `oint E.dl` over the rectangular loop 1234 shown in figure.
- Evaluate `int B.ds` over the surface bounded by loop 1234.
- Use equation `oint E.dl = (-dphi_B)/(dt)` to prove `E_0/B_0` = c.
- By using similar process and the equation `ointB.dl = mu_0I + ε_0 (dphi_E)/(dt)`, prove that c = `1/sqrt(mu_0ε_0)`
उत्तर
i. Let electromagnetic wave is propagating along z-axis, in the case electric field vector `(vecE)` be along x-axis and magnetic field vector `(vecB)` along y-axis i.e., `vecE = E_0 hati` and `vecB = B_0 hatj`.
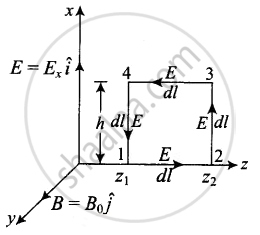
The line integral of `vecE` over the closed rectangular path 1234 in x-z plane of the figure is
`ointvecE*dvecl = int_1^2 vecE*dvecl + int_2^3 vecE*dvecl + int_3^4 vecE*dvecl + int_4^1 vecE*dvecl`
= `int_1^2 E*dl cos 90° + int_2^3 E*dl cos 0° + oint_3^4 E*dl cos 90° + int_4^1 E*dl cos 180°`
`oint vecE*dvecl = E_0h [sin (kz_2 - ωt) - sin(kz_1 - ωt)` .....(i)
ii. Now let us evaluate `int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of are `ds = hdz` each.
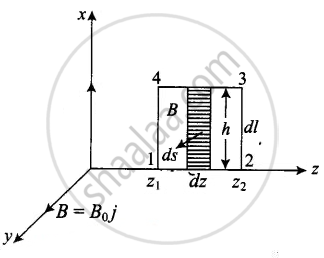
`int vecB * dvecs = int B*ds cos 0 = int B*ds`
= `int_(Z_1)^(Z_2) B_0 sin (kz - ωt)hdz`
`int vecB*dvecs = (-B_0h)/k [cos (kz_2 - ωt) - cos (kz_2 - ωt)]` ......(ii)
iii. We are given `ointE*dl = (-dphi_B)/(dt) = - d/(dt) oint B*ds`
Substituting the values from equation (i) and (ii), we get
`E_0h [sin (kz - ωt) - sin (kz_1 - ωt)] = (-d)/(dt) [(B_0h)/k cos (kz - ωt) - cos (kz_1 - ωt)]`
= `(B_0h)/k ω [sin (kz_2 - ωt) - sin (kz_1 - ωt)]`
⇒ `E_0 = (B_0ω)/k = B_0c` .....`[because ω/k = c]`
⇒ `E_0/B_0 = c`
iv. For evaluating `oint vecB.dvecl`, let us consider a loop 1234 in y-z plane as shown in figure given below.
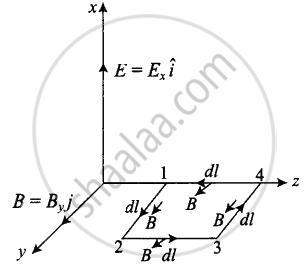
`oint vecB*dvecl = int_1^2 vecB*dvecl + int_2^3 vecB*dvecl + int_3^4 vecB*dvecl + int_4^1 vecB*dvecl`
= `int_1^2 B*dl cos 0° + int_2^3 B*dl cos 90° + int_3^4 B*dl cos 180° + int_4^1 B*dl cos 90°`
`oint vecB*dvecl = B_0h [sin (kz - ωt) - sin (kz_1 - ωt)]` ......(iii)
Now to evaluate `phi_E = int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of area hds each.
`phi_E = int vecE*dvecs = int Eds cos 0 = int Eds`
= `int_(z_1)^z E_0 sin (kz_1 - ωt)hdz`
`oint vecE * dvecs = - (E_0h)/k [cos (kz_2 - ωt) - cos (kz_1 - ωt)]`
∴ `(dphi_E)/(dt) = (E_0hω)/k [sin (kz_1 - ωt) - sin (kz_2 - ωt)]` .....(iv)
Let `oint B*dl = mu_0(I + (ε_0dphi_E)/(dt))` where I = conduction current = 0 in vacuum
∴ `oint B*dl = mu_0ε (dphi_E)/(dt)`
Using relations obtained in equation (iii) and (iv) and simplifying, we get
`B_0 = E_0 (ωmu_0ε_0)/k`
⇒ `E_0/B_0 ω/k = 1/(mu_0ε_0)`
But `E_0/B_0 = c` and `ω = ck` ⇒ `c*c = 1/(mu_0ε_0)`,
Therefore `c = = 1/(mu_0ε_0)`
APPEARS IN
संबंधित प्रश्न
Arrange the following electromagnetic wave in the order of their increasing wavelength:
(a) γ- rays
(b) Microwaves
(c) X-rays
(d) Radio waves
Draw a schematic sketch of the electromagnetic waves propagating along the + x-axis. Indicate the directions of the electric and magnetic fields
Do electromagnetic waves carry energy and momentum ?
How does a charge q oscillating at certain frequency produce electromagnetic waves?
Sketch a schematic diagram depicting electric and magnetic fields for an electromagnetic wave propagating along the Z-direction.
The electric and magnetic fields, associated with an electromagnetic wave, propagating along negative X-axis can be represented by ______.
Wavelength λ and wave vector k are related by ______.
A man standing on the road has to hold his umbrella at 30° with the vertical to keep the rain away. He throws away the umbrella and starts, running at 10 km/h and finds raindrops hitting his head vertically. The speed of the raindrops with respect to the road is ______.
Why is the orientation of the portable radio with respect to broadcasting station important?
A plane electromagnetic wave, has frequency of 2.0 × 1010 Hz and its energy density is 1.02 × 10-8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close to `(1/(4piepsilon_0) = 9xx10^9"Nm"^2/"C"^2 "and speed of light" = 3 xx 10^8 "m" "s"^-1)`:
The electric field in a plane electromagnetic wave is given by `vecE = 200cos[((0.5 xx 10^3)/m)x - (1.5 xx 10^11 "rad"/s xx t)]V/mhatj`. If the wave falls normally on a perfectly reflecting surface having an area of 100 cm2. If the radiation pressure exerted by the E.M. wave on the surface during a 10-minute exposure is `x/10^9 N/m^2`. Find the value of x.
