Advertisements
Advertisements
Question
A plane EM wave travelling in vacuum along z direction is given by `E = E_0 sin(kz - ωt)hati` and `B = B_0 sin(kz - ωt)hatj`
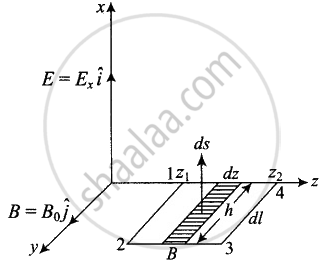
- Evaluate `oint E.dl` over the rectangular loop 1234 shown in figure.
- Evaluate `int B.ds` over the surface bounded by loop 1234.
- Use equation `oint E.dl = (-dphi_B)/(dt)` to prove `E_0/B_0` = c.
- By using similar process and the equation `ointB.dl = mu_0I + ε_0 (dphi_E)/(dt)`, prove that c = `1/sqrt(mu_0ε_0)`
Solution
i. Let electromagnetic wave is propagating along z-axis, in the case electric field vector `(vecE)` be along x-axis and magnetic field vector `(vecB)` along y-axis i.e., `vecE = E_0 hati` and `vecB = B_0 hatj`.
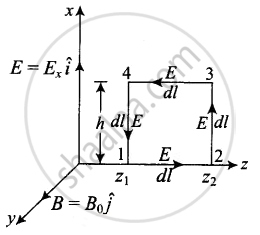
The line integral of `vecE` over the closed rectangular path 1234 in x-z plane of the figure is
`ointvecE*dvecl = int_1^2 vecE*dvecl + int_2^3 vecE*dvecl + int_3^4 vecE*dvecl + int_4^1 vecE*dvecl`
= `int_1^2 E*dl cos 90° + int_2^3 E*dl cos 0° + oint_3^4 E*dl cos 90° + int_4^1 E*dl cos 180°`
`oint vecE*dvecl = E_0h [sin (kz_2 - ωt) - sin(kz_1 - ωt)` .....(i)
ii. Now let us evaluate `int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of are `ds = hdz` each.
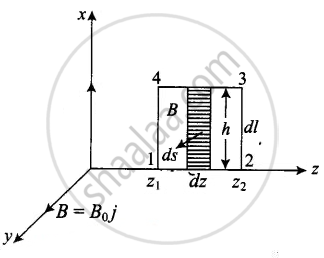
`int vecB * dvecs = int B*ds cos 0 = int B*ds`
= `int_(Z_1)^(Z_2) B_0 sin (kz - ωt)hdz`
`int vecB*dvecs = (-B_0h)/k [cos (kz_2 - ωt) - cos (kz_2 - ωt)]` ......(ii)
iii. We are given `ointE*dl = (-dphi_B)/(dt) = - d/(dt) oint B*ds`
Substituting the values from equation (i) and (ii), we get
`E_0h [sin (kz - ωt) - sin (kz_1 - ωt)] = (-d)/(dt) [(B_0h)/k cos (kz - ωt) - cos (kz_1 - ωt)]`
= `(B_0h)/k ω [sin (kz_2 - ωt) - sin (kz_1 - ωt)]`
⇒ `E_0 = (B_0ω)/k = B_0c` .....`[because ω/k = c]`
⇒ `E_0/B_0 = c`
iv. For evaluating `oint vecB.dvecl`, let us consider a loop 1234 in y-z plane as shown in figure given below.
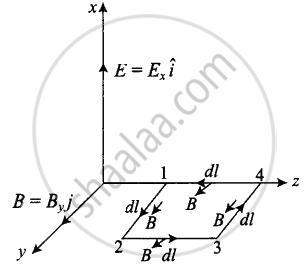
`oint vecB*dvecl = int_1^2 vecB*dvecl + int_2^3 vecB*dvecl + int_3^4 vecB*dvecl + int_4^1 vecB*dvecl`
= `int_1^2 B*dl cos 0° + int_2^3 B*dl cos 90° + int_3^4 B*dl cos 180° + int_4^1 B*dl cos 90°`
`oint vecB*dvecl = B_0h [sin (kz - ωt) - sin (kz_1 - ωt)]` ......(iii)
Now to evaluate `phi_E = int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of area hds each.
`phi_E = int vecE*dvecs = int Eds cos 0 = int Eds`
= `int_(z_1)^z E_0 sin (kz_1 - ωt)hdz`
`oint vecE * dvecs = - (E_0h)/k [cos (kz_2 - ωt) - cos (kz_1 - ωt)]`
∴ `(dphi_E)/(dt) = (E_0hω)/k [sin (kz_1 - ωt) - sin (kz_2 - ωt)]` .....(iv)
Let `oint B*dl = mu_0(I + (ε_0dphi_E)/(dt))` where I = conduction current = 0 in vacuum
∴ `oint B*dl = mu_0ε (dphi_E)/(dt)`
Using relations obtained in equation (iii) and (iv) and simplifying, we get
`B_0 = E_0 (ωmu_0ε_0)/k`
⇒ `E_0/B_0 ω/k = 1/(mu_0ε_0)`
But `E_0/B_0 = c` and `ω = ck` ⇒ `c*c = 1/(mu_0ε_0)`,
Therefore `c = = 1/(mu_0ε_0)`
APPEARS IN
RELATED QUESTIONS
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B0 = 510 nT. What is the amplitude of the electric field part of the wave?
About 5% of the power of a 100 W light bulb is converted to visible radiation. What is the average intensity of visible radiation
(a) at a distance of 1 m from the bulb?
(b) at a distance of 10 m?
Assume that the radiation is emitted isotropically and neglect reflection.
Which segment of electromagnetic waves has highest frequency? How are these waves produced? Give one use of these waves.
Explain briefly how electromagnetic waves are produced by an oscillating charge. How is the frequency of the em waves produced related to that of the oscillating charge?
The energy levels of an atom of a certain element are shown in the given figure. Which one of the transitions A, B, C, D or E will result in the emission of photons of electromagnetic radiation of wavelength 618.75 nm? Support your answer with mathematical calculations.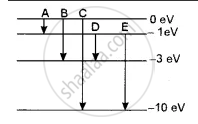
The electric and magnetic fields of an electromagnetic wave are ______.
Discuss the source of electromagnetic waves.
Plane electromagnetic waves are ______.
A plane electromagnetic wave propagating along x direction can have the following pairs of E and B.
- Ex, By.
- Ey, Bz.
- Bx, Ey.
- Ex, By.
A plane electromagnetic wave, has frequency of 2.0 × 1010 Hz and its energy density is 1.02 × 10-8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close to `(1/(4piepsilon_0) = 9xx10^9"Nm"^2/"C"^2 "and speed of light" = 3 xx 10^8 "m" "s"^-1)`:
