Question

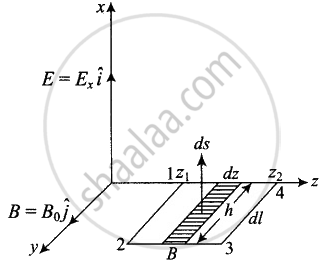
A plane EM wave travelling in vacuum along z direction is given by `E = E_0 sin(kz - ωt)hati` and `B = B_0 sin(kz - ωt)hatj` 

1. Evaluate `oint E.dl` over the rectangular loop 1234 shown in figure.
2. Evaluate `int B.ds` over the surface bounded by loop 1234.
3. Use equation `oint E.dl = (-dphi_B)/(dt)` to prove `E_0/B_0` = c.
4. By using similar process and the equation `ointB.dl = mu_0I + ε_0 (dphi_E)/(dt)`, prove that c = `1/sqrt(mu_0ε_0)`

Answer 1

i. Let electromagnetic wave is propagating along z-axis, in the case electric field vector `(vecE)` be along x-axis and magnetic field vector `(vecB)` along y-axis i.e., `vecE = E_0 hati` and `vecB = B_0 hatj`.

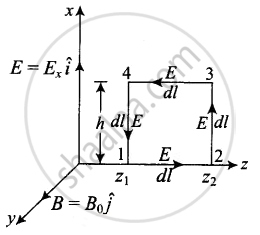
The line integral of `vecE` over the closed rectangular path 1234 in x-z plane of the figure is

`ointvecE*dvecl = int_1^2 vecE*dvecl + int_2^3 vecE*dvecl + int_3^4 vecE*dvecl + int_4^1 vecE*dvecl`

= `int_1^2 E*dl cos 90° + int_2^3 E*dl cos 0° + oint_3^4 E*dl cos 90° + int_4^1 E*dl cos 180°`

`oint vecE*dvecl = E_0h [sin (kz_2 - ωt) - sin(kz_1 - ωt)`  .....(i)

ii. Now let us evaluate `int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of are `ds = hdz` each.

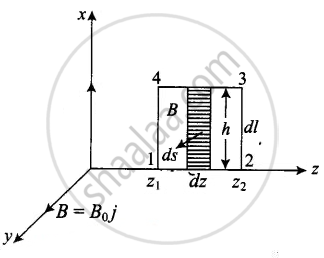
`int vecB * dvecs = int B*ds cos 0 = int B*ds`

= `int_(Z_1)^(Z_2) B_0 sin (kz - ωt)hdz`

`int vecB*dvecs = (-B_0h)/k [cos (kz_2 - ωt) - cos (kz_2 - ωt)]`  ......(ii)

iii. We are given `ointE*dl = (-dphi_B)/(dt) = - d/(dt) oint B*ds`

Substituting the values from equation (i) and (ii), we get

`E_0h [sin (kz - ωt) - sin (kz_1 - ωt)] = (-d)/(dt) [(B_0h)/k cos (kz - ωt) - cos (kz_1 - ωt)]`

= `(B_0h)/k ω [sin (kz_2 - ωt) - sin (kz_1 - ωt)]`

⇒ `E_0 = (B_0ω)/k = B_0c`  .....`[because ω/k = c]`

⇒ `E_0/B_0 = c`

iv. For evaluating `oint vecB.dvecl`, let us consider a loop 1234 in y-z plane as shown in figure given below.

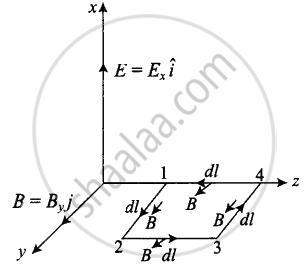
`oint vecB*dvecl = int_1^2 vecB*dvecl + int_2^3 vecB*dvecl + int_3^4 vecB*dvecl + int_4^1 vecB*dvecl`

= `int_1^2 B*dl cos 0° + int_2^3 B*dl cos 90° + int_3^4 B*dl cos 180° + int_4^1 B*dl cos 90°`

`oint vecB*dvecl = B_0h [sin (kz - ωt) - sin (kz_1 - ωt)]`  ......(iii)

Now to evaluate `phi_E = int vecB*dvecs`, let us consider the rectangle 1234 to be made of strips of area hds each.

`phi_E = int vecE*dvecs = int Eds cos 0 = int Eds`

= `int_(z_1)^z E_0 sin (kz_1 - ωt)hdz`

`oint vecE * dvecs = - (E_0h)/k [cos (kz_2 - ωt) - cos (kz_1 - ωt)]`

∴ `(dphi_E)/(dt) = (E_0hω)/k [sin (kz_1 - ωt) - sin (kz_2 - ωt)]`  .....(iv)

Let `oint B*dl = mu_0(I + (ε_0dphi_E)/(dt))` where I = conduction current = 0 in vacuum

∴ `oint B*dl = mu_0ε (dphi_E)/(dt)`

Using relations obtained in equation (iii) and (iv) and simplifying, we get

`B_0 = E_0 (ωmu_0ε_0)/k`

⇒ `E_0/B_0 ω/k = 1/(mu_0ε_0)`

But `E_0/B_0 = c` and `ω = ck` ⇒ `c*c = 1/(mu_0ε_0)`,

Therefore `c = = 1/(mu_0ε_0)`