Question

A long straight cable of length `l` is placed symmetrically along z-axis and has radius a(<< l). The cable consists of a thin wire and a co-axial conducting tube. An alternating current I(t) = I₀ sin (2πνt) flows down the central thin wire and returns along the co-axial conducting tube. The induced electric field at a distance s from the wire inside the cable is E(s,t) = µ₀I₀ν cos (2πνt) In `(s/a)hatk`.

1. Calculate the displacement current density inside the cable.
2. Integrate the displacement current density across the cross-section of the cable to find the total displacement current I^d.
3. Compare the conduction current I0 with the displacement current `I_0^d`.

Answer 1

i. Induced electric field E(s, t) at distance s(s < radius of co-axial cable) is given as E(s, t) = ε₀I₀v cos 2πνt `log_e (s/a) hatk`. Displacement current density I_d is given by

J_d = `ε_0 (dE)/(dt) = ε_0mu_0I_0 v d/(dt) [cos 2πνt. log_e (s/a)]hatk`

J_d = `ε_0mu_0I_0v [(- sin 2πνt) .2πν. log_e (s/a)]hatk`  ......[∵ s and a are constant]

J_d = `-ε_0mu_0I_02πν^2 log_e (s/a) (sin 2πνt) hatk`

= `-1/C_0 I_02πν^2 log_e (a*s) (sin 2πνt) hatk` ......`[∵ C = 1/sqrt(mu_0ε_0)]`

= `+ (2πν^2)/C^2 I_0 log_e (a/s) sin 2πνt hatk`

= `(2πν^2)/(v^2λ^2) I_0 log_e (a/s) sin 2πνhatk`

Jd = `(2πl_0)/λ^2 log_e  a/s sin(2πνt)hatk`

ii. Total displacement current, `I^d = int J_d 2πsds`

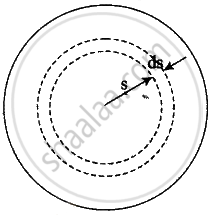
`I^d = int_0^a ((2piI_0)/λ^2  "In"  a/s sin 2πνt)2πsds`

= `int_0^a [(2pi)/λ^2 I_0 int_(s = 0)^a  "In"  (a/s)sds sin 2πvt] xx 2π`

= `((2π)/λ)^2 I_0 int_0^a  "In"  (a/s) 1/2d(s^2)* sin 2πvt`

= `(a/2)^2 ((2π)/λ)^2 I_0 sin 2πvt int_0^a  "In"  (a/s)*d(s/a)^2`

= `a^2/4 ((2π)/λ)^2 I_0 sin 2πvt int_0^a  "In"  (a/s)*d(s/a)^2`

= `a^2/4 ((2π)/λ)^2 I_0 sin 2πvt xx (1)`  .....`[∵ int_(s = 0)^a  "In"  (s/a)^2 d(s/d)^2 = 1]`

∴ `I_d = a^2/4 ((2π)/λ)^2 I_0 sin 2πvt`

⇒ `I_d = ((πa)/λ)^2 I_0 sin 2πvt`

iii. The displacement current,

I^d = `((πa)/λ)^2 I_0 sin 2πvt = I_0^d sin 2πvt`

Here, `I_0^d ((aπ)/λ)^2 I_0`

⇒ `I_0^d/I_0 = ((aπ)/λ)^2`