Advertisements
Advertisements
प्रश्न
A ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40°. If the angle of emergence is 60°, calculate the angle of the prism.
उत्तर
Given :
`mu = 1.52` `i = 40^circ`
`e = 60^circ` A = ?
`mu = sin i/sin r`
`1.52 = sin 40^circ/sin r`
`therefore sin r = 0.6427/1.52`
`sin r = 0.4228`
`therefore r = sin^-1(0.4228)`
`r = 25.01^circ`
`1/mu = (sin r')/sin e ⇒ sin r' = sin e/mu`
⇒ `sin r' = sin 60^circ/1.52 = 0.866/1.52 = 0.57`
⇒ `r' = sin^-1(0.57) = 34.75^circ`
`therefore A = r + r' = 25.01^circ + 34.75^circ = 59.76^circ`
APPEARS IN
संबंधित प्रश्न
Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of the prism.
A ray of light passes through an equilateral glass prism such that the angle of incidence is equal to the angle of emergence and each of these angles is equal to 3/4 of angle of prism. Find the angle of deviation.
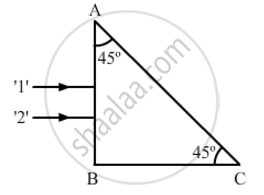
Two monochromatic rays of light are incident normally on the face AB of an isosceles right-angled prism ABC. The refractive indices of the glass prism for the two rays '1' and '2' are respectively 1.38 and 1.52. Trace the path of these rays after entering through the prism.
State any two difference between the primary rainbow and secondary rainbow
For any prism, prove that :
'n' or `mu = sin((A + delta_m)/2)/sin(A/2)`
where the terms have their usual meaning
The equation \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] was derived for a prism having small refracting angle. Is it also valid for a prism of large refracting angle? Is it also valid for a glass slab or a glass sphere?
By properly combining two prisms made of different materials, it is possible to
(a) have dispersion without average deviation
(b) have deviation without dispersion
(c) have both dispersion and average deviation
(d) have neither dispersion nor average deviation
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
A thin prism of crown glass (μr = 1.515, μv = 1.525) and a thin prism of flint glass (μr = 1.612, μv = 1.632) are placed in contact with each other. Their refracting angles are 5.0° each and are similarly directed. Calculate the angular dispersion produced by the combination.
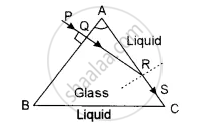
A narrow beam of monochromatic light, PQ, is incident normally on one face of an equiangular glass prism of refractive index 1.45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (See figure). Find the refractive index of this liquid.