Advertisements
Advertisements
प्रश्न
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
उत्तर
The refractive indices for red and yellow lights are μr = 1.61 and μy = 1.65, respectively.
Dispersive power, ω = 0.07
Angle of minimum deviation, δy = 4°
Now, using the relation \[\omega = \frac{\mu_v - \mu_r}{\mu_y - 1},\] we get
\[ \Rightarrow 0 . 07 = \frac{1 . 65 - 1 . 61}{\mu_y - 1}\]
\[\Rightarrow \mu_y - 1 = \frac{0 . 04}{0 . 07} = \frac{4}{7}\]
Let the angle of the prism be A.
Angle of minimum deviation, δ = (μ − 1)A
\[\Rightarrow A = \frac{\delta_y}{\mu_y - 1} = \frac{4}{\left( \frac{4}{7} \right)} = 7^\circ\]
Thus, the angle of the prism is 7°.
APPEARS IN
संबंधित प्रश्न
Plot a graph to show the variation of the angle of deviation as a function of the angle of incidence for light passing through a prism. Derive an expression for the refractive index of the prism in terms of angle of minimum deviation and angle of the prism.
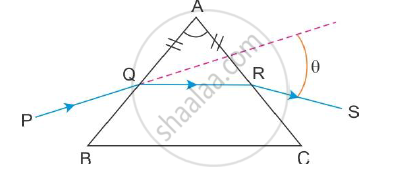
A ray PQ incident on the refracting face BA is refracted in the prism BAC as shown in the figure and emerges from the other refracting face AC as RS such that AQ = AR. If the angle of prism A = 60° and refractive index of material of prism is `sqrt3 `. Calculate angle θ.
What is a dispersion of light
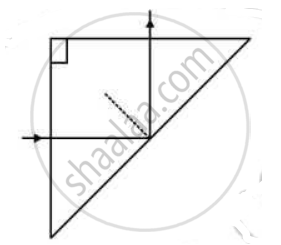
A ray of light incident normally on one face of a right isosceles prism is totally reflected, as shown in fig. What must be the minimum value of refractive index of glass? Give relevant calculations.
For any prism, prove that :
'n' or `mu = sin((A + delta_m)/2)/sin(A/2)`
where the terms have their usual meaning
Draw the ray diagram showing refraction of light through a glass prism and hence obtain the relation between the refractive index μ of the prism, angle of prism and angle of minimum deviation.
Give the formula that can be used to determine refractive index of materials of a prism in minimum deviation condition ?
If three identical prisms are combined, is it possible to pass a beam that emerges undeviated? Undispersed?
A prism can produce a minimum deviation δ in a light beam. If three such prisms are combined, the minimum deviation that can be produced in this beam is _______________.
The minimum deviations suffered by, yellow and violet beams passing through an equilateral transparent prism are 38.4°, 38.7° and 39.2° respectively. Calculate the dispersive power of the medium.
Two prisms of identical geometrical shape are combined with their refracting angles oppositely directed. The materials of the prisms have refractive indices 1.52 and 1.62 for violet light. A violet ray is deviated by 1.0° when passes symmetrically through this combination. What is the angle of the prisms?
A ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40°. If the angle of emergence is 60°, calculate the angle of the prism.
A narrow beam of monochromatic light, PQ, is incident normally on one face of an equiangular glass prism of refractive index 1.45. When the prism is immersed in a certain liquid, the ray makes a grazing emergence along the other face (See figure). Find the refractive index of this liquid. 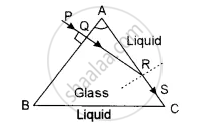
What is meant by the dispersive power of transparent material?
Prove that in case of a prism, i + e = A + δ, where the symbols have their usual meanings.
What is meant by a thin prism?
