Advertisements
Advertisements
प्रश्न
What is meant by a thin prism?
उत्तर
It is that prism whose refracting angle is small i.e., less than 4°.
APPEARS IN
संबंधित प्रश्न
A ray PQ incident on the face AB of a prism ABC, as shown in the figure, emerges from the face AC such that AQ = AR.
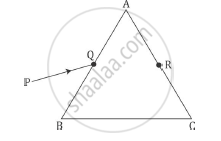
Draw the ray diagram showing the passage of the ray through the prism. If the angle of the prism is 60° and refractive index of the material of prism is `sqrt3` , determine the values of angle of incidence and angle of deviation
What is the cause of dispersion of light
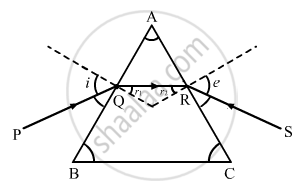
Figure shows a ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, show that (i) r1 = r2 = A/2 and (ii) angle of minimum deviation, Dm = 2i − A.
Can the dispersive power \[\omega = \frac{\mu_u - \mu_r}{\mu - 1}\] be negative? What is the sign of ω if a hollow prism is immersed into water?
If a glass prism is dipped in water, its dispersive power ___________ .
A thin prism is made of a material having refractive indices 1.61 and 1.65 for red and violet light. The dispersive power of the material is 0.07. It is found that a beam of yellow light passing through the prism suffers a minimum deviation of 4.0° in favourable conditions. Calculate the angle of the prism.
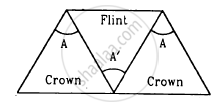
Three thin prisms are combined as shown in figure. The refractive indices of the crown glass for red, yellow and violet rays are μr, μy and μv respectively and those for the flint glass are μ'r, μ'y and μ'v respectively. Find the ratio A'/A for which (a) there is no net angular dispersion, and (b) there is no net deviation in the yellow ray.
A thin prism of angle 6.0°, ω = 0.07 and μy = 1.50 is combined with another thin prism having ω = 0.08 and μy = 1.60. The combination produces no deviation in the mean ray. (a) Find the angle of the second prism. (b) Find the net angular dispersion produced by the combination when a beam of white light passes through it. (c) If the prisms are similarly directed, what will be the deviation in the mean ray? (d) Find the angular dispersion in the situation described in (c).
Prove that in case of a prism, i + e = A + δ, where the symbols have their usual meanings.
When a ray of white light is incident obliquely on the first surface of a prism, then ______.
