Advertisements
Advertisements
प्रश्न
A series LCR circuit is connected to a source having voltage v = vm sin ωt. Derive the expression for the instantaneous current I and its phase relationship to the applied voltage.
Obtain the condition for resonance to occur. Define ‘power factor’. State the conditions under which it is (i) maximum and (ii) minimum.
उत्तर
v = vm sin ωt
Let the current in the circuit be led the applied voltage by an angleΦ.
`i= i_m sin(omegat +phi)`
The Kirchhoff’s voltage law gives`L ((di)/dt +Ri +q/C = v)`.
It is given that v = vm sin ωt (applied voltage)
`L(d^2q)/(dt^2) +R(dq)/(dt) +q/C = v_m sinomegat ...... (1)`
On solving the equation, we obtain
`q = q_m sin(omegat + theta)`
`(dp)/(dt) = q_momega cos(omegat +theta)`
`((d^2)q)/(dt^2) = -q_momega^2 sin(omegat +theta)`
On substituting these values in equation (1), we obtain
`q_momega[R cos(omegat +theta)+ (X_c -X_L)sin(omegat +theta)] = v_msinomegat`
`X_c = 1/(omegaC) X_c = omegaL`
`Z = sqrt(R^2 +(X_c - X_L)^2`
`q_momegaZ[R/Z cos(omegat+theta)+((X_c -X_L))/Z sin (omegat+theta)] = v_m sin omegat ........... (2)`
Let `cos phi = R/2` and `(X_c -X_L)/Z = sinphi`
This gives
`tan phi = (X_c - X_L)/R`
On substituting this in equation (2), we obtain
`q_momegaZcos (omegat +theta -phi) = v_msinomegat`
On comparing the two sides, we obtain
`V_m = q_momegaZ = i+mZ`
`i_m = q_momega`
and `(theta-phi) = -pi/2`
`I = (dp)/(dt ) =q_momega cos (omegat+theta)`
`=i_m cos(omegat+theta)`
Or
`i = i_m sin(omegat +theta)`
Where,`i_m = (v_m)/Z = (v_m)/(sqrt(R^2 +(X_c - X_L)^2)`
And
`phi = tan^-1((X_c -X_L)/R)`
The condition for resonance to occur
`i_m = v_m/sqrt(R^2 +(X_C - X_L)^2)`
For resonance to occur, the value of im has to be the maximum.
The value of im will be the maximum when
`X_c = X_L`
`1/(omega C) = omegaL`
`omega^2 = 1/(LC)`
`omega = 1/(sqrtLC)`
`2pif = 1/sqrt(LC)`
`f = 1/(02pisqrt(LC)`
Power factor = cos Φ
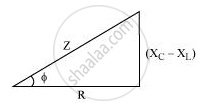
Where,`cosphi = R/Z = R/(sqrt(R^2 +(X_c- X_L)^2)`
(i) Conditions for maximum power factor (i.e., cos Φ = 1)
-
XC = XL
Or
-
R = 0
(ii) Conditions for minimum power factor
-
When the circuit is purely inductive
-
When the circuit is purely capacitive
APPEARS IN
संबंधित प्रश्न
Derive an expression for the average power consumed in a series LCR circuit connected to a.c. source in which the phase difference between the voltage and the current in the circuit is Φ.
Answer the following question.
In a series LCR circuit connected across an ac source of variable frequency, obtain the expression for its impedance and draw a plot showing its variation with frequency of the ac source.
Choose the correct answer from given options
The selectivity of a series LCR a.c. circuit is large, when
A series LCR circuit with L = 0.12 H, C = 480 nF, R = 23 Ω is connected to a 230 V variable frequency supply.
(a) What is the source frequency for which current amplitude is maximum. Obtain this maximum value.
(b) What is the source frequency for which average power absorbed by the circuit is maximum. Obtain the value of this maximum power.
(c) For which frequencies of the source is the power transferred to the circuit half the power at resonant frequency? What is the current amplitude at these frequencies?
(d) What is the Q-factor of the given circuit?
In series combination of R, L and C with an A.C. source at resonance, if R = 20 ohm, then impedence Z of the combination is ______.
At resonant frequency the current amplitude in series LCR circuit is ______.
A series LCR circuit driven by 300 V at a frequency of 50 Hz contains a resistance R = 3 kΩ, an inductor of inductive reactance XL = 250 πΩ, and an unknown capacitor. The value of capacitance to maximize the average power should be ______.
A series LCR circuit containing a resistance of 120 Ω has angular resonance frequency 4 × 105 rad s-1. At resonance the voltage across resistance and inductance are 60 V and 40 V respectively. At what frequency the current in the circuit lags the voltage by 45°. Give answer in ______ × 105 rad s-1.
Select the most appropriate option with regard to resonance in a series LCR circuit.
